题目内容
19.已知函数y=ln(x2+ax-1+2a)的值域为R,则a的取值范围是(-∞,4-2$\sqrt{3}$]∪[4+2$\sqrt{3}$,+∞).分析 可以令f(x)=x2+ax-1+2a,由题意函数的值域为R,则可得f(x)可以取所有的正数可得,△≥0,解不等式即可求解.
解答 解:∵函数y=ln(x2+ax-1+2a)的值域为R,
∴f(x)=x2+ax-1+2a可以取所有的正数可得,△≥0,
∴a2-4(2a-1)≥0,
解得a≥4+2$\sqrt{3}$或a≤4-2$\sqrt{3}$,
故答案为:(-∞,4-2$\sqrt{3}$]∪[4+2$\sqrt{3}$,+∞).
点评 本题主要考查了由二次函数与对数函数复合的复合函数,解题的关键是要熟悉对数函数的性质,解题时容易误认为△<0,要注意区别与函数的定义域为R的限制条件.

练习册系列答案
相关题目
9.某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:
(1)求广告费支出x与销售额y回归直线方程$\hat y$=bx+a(a,b∈R);
已知b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
已知b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
7.设A、B为两个独立事件,若P(A)=0.4,P(A∪B)=0.7.则P(B)=( )
| A. | 0.6 | B. | 0.5 | C. | 0.4 | D. | 0.3 |
11.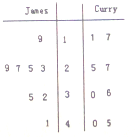 如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )
如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )
 如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )
如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )| A. | 他们的水平相当,但James 比Curry发挥稳定 | |
| B. | 他们的水平相当,但Curry比James 发挥稳定 | |
| C. | James比Curry水平高,也比Curry发挥稳定 | |
| D. | Curry比水平高,也比James发挥稳定 |
8.若函数f(x)=ax2+ax-1对?x∈R都有f(x)<0恒成立,则实数a的取值范围是( )
| A. | -4<a≤0 | B. | a<-4 | C. | -4<a<0 | D. | a≤0 |