题目内容
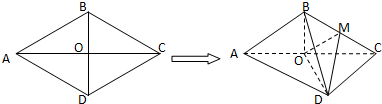
如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形沿对角线AC折起,使得平面ABC⊥平面ADC,得到三棱锥B-ACD,M是棱BC上的一点.
(Ⅰ)若OM⊥BC,求证:BC⊥平面OMD;
(Ⅱ)若OM∥平面ABD,求三棱锥M-ABD的体积.

(Ⅰ)若OM⊥BC,求证:BC⊥平面OMD;
(Ⅱ)若OM∥平面ABD,求三棱锥M-ABD的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)利用OM⊥BC,通过证明OD⊥BC,利用直线与平面垂直的判定定理证明BC⊥平面OMD;
(Ⅱ)若OM∥平面ABD,说明OD为三棱锥D-ABM的高,求出△ABM的面积,即可求三棱锥M-ABD的体积.
(Ⅱ)若OM∥平面ABD,说明OD为三棱锥D-ABM的高,求出△ABM的面积,即可求三棱锥M-ABD的体积.
解答:
解:(Ⅰ)证明∵平面ABC⊥平面ADC
又∵在菱形中,OD⊥AC
而平面ABC∩平面ADC=AC∴OD⊥平面ABC----------------(3分)
又∵BC?平面ABC∴OD⊥BC.
又∵OM⊥BC,OM∩OD=0.
∴BC⊥平面OMD---------------(6分)
(Ⅱ)∵OM∥平面ABD
又∵OM?平面ABC,平面ABC∩平面ABD=AB∴OM∥AB
又∵O为AC中点∴M为AC中点---------(9分)
由(Ⅰ)可知OD⊥面ABC
即OD为三棱锥D-ABM的高----------(10分)
在△ABM中,AB=6,∠ABC=120°,BM=3,
∴S△ABM=
×3×6×sin120°=
.
VM-ABD=VD-ABM=
S△ABM×OD=
×
×3=
-----------(12分)
又∵在菱形中,OD⊥AC
而平面ABC∩平面ADC=AC∴OD⊥平面ABC----------------(3分)
又∵BC?平面ABC∴OD⊥BC.
又∵OM⊥BC,OM∩OD=0.
∴BC⊥平面OMD---------------(6分)
(Ⅱ)∵OM∥平面ABD
又∵OM?平面ABC,平面ABC∩平面ABD=AB∴OM∥AB
又∵O为AC中点∴M为AC中点---------(9分)
由(Ⅰ)可知OD⊥面ABC
即OD为三棱锥D-ABM的高----------(10分)
在△ABM中,AB=6,∠ABC=120°,BM=3,
∴S△ABM=
| 1 |
| 2 |
| 9 |
| 2 |
| 3 |
VM-ABD=VD-ABM=
| 1 |
| 3 |
| 1 |
| 3 |
| 9 |
| 2 |
| 3 |
| 9 |
| 2 |
| 3 |
点评:本题考查直线与平面垂直的判定定理的与,几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目