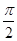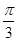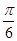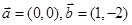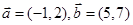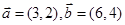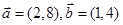题目内容
已知向量 ,
, 满足|
满足| |=2,|
|=2,| |=3,|2
|=3,|2 +
+ |=
|=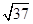 ,则
,则 与
与 的夹角为
的夹角为
| A.30° | B.45° | C.60° | D.90° |
C
解析试题分析:因为向量 ,
, 满足|
满足| |=2,|
|=2,| |=3,|2
|=3,|2 +
+ |=
|=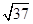 ,所以|2
,所以|2 +
+ |
|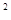 =37,即4|
=37,即4| |
|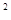 +|
+| |
|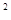 +4
+4 ·
· =37,所以
=37,所以 ·
· =3,
=3,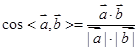 =
=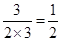 ,又
,又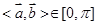 ,所以,
,所以,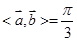 ,故选C。
,故选C。
考点:本题主要考查平面向量模的概念,数量积及夹角运算。
点评:中档题,涉及平面向量模的计算问题,往往要“化模为方”,将实数运算转化成向量的数量积。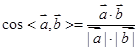

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
设点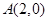 ,
,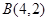 ,若点
,若点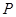 在直线
在直线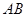 上,且
上,且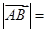
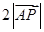 ,则点
,则点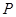 的坐标为( )
的坐标为( )
A.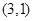 | B.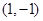 | C.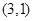 或 或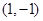 | D.无数多个 |
已知平行四边形ABCD的三个顶点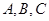 的坐标分别是
的坐标分别是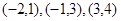 ,则向量
,则向量 的坐标是( )
的坐标是( )
A.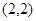 | B.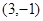 | C.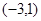 | D.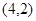 |
设两个向量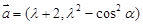 和
和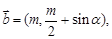 其中
其中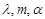 为实数.若
为实数.若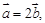 则
则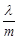 的取值范围是 ( )
的取值范围是 ( )
A.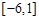 | B.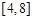 | C. | D. |
若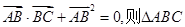 是 ( )
是 ( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.等腰直角三角形 |
设P是 所在平面上一点,且满足
所在平面上一点,且满足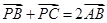 ,若
,若 的面积为1,则
的面积为1,则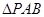 的面积为( )
的面积为( )
A.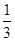 | B. | C.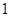 | D.2 |
设向量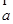 =(1,-3),
=(1,-3), 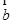 =(-2,4),
=(-2,4), 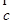 =(-1,-2),若表示向量4
=(-1,-2),若表示向量4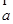 ,4
,4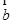 -2
-2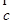 ,2(
,2(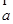 -
-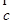 ),
),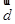 的有向线段首尾相连能构成四边形,则向量
的有向线段首尾相连能构成四边形,则向量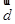 为( )
为( )
| A.(2,6) | B.(-2,6) | C.(2,-6) | D.(-2,-6) |
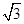 ,且|2a+b|=
,且|2a+b|=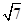 ,则向量a与向量a+b的夹角为( )
,则向量a与向量a+b的夹角为( )