题目内容
设点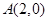 ,
,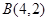 ,若点
,若点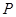 在直线
在直线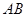 上,且
上,且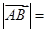
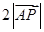 ,则点
,则点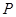 的坐标为( )
的坐标为( )
A.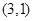 | B.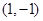 | C.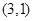 或 或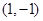 | D.无数多个 |
C
解析试题分析:根据题意,由于点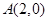 ,
,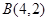 ,则直线AB:y=x-2,若点
,则直线AB:y=x-2,若点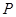 在直线
在直线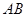 上,且
上,且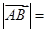
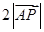 ,则可知点P是AB的中点或者是AB的延长线上一点,那么可知点P的坐标为
,则可知点P是AB的中点或者是AB的延长线上一点,那么可知点P的坐标为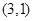 或
或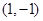 ,故答案为C.
,故答案为C.
考点:向量的坐标运算
点评:主要是考查了向量的概念以及线性运算,属于基础题。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
如果向量 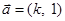 与
与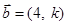 共线且方向相反,则
共线且方向相反,则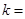 ( ).
( ).
A.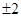 | B.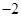 | C.2 | D.0 |
已知向量 ,且
,且 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
定义平面向量之间的一种运算“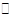 ”如下,对任意的
”如下,对任意的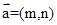 ,
,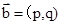 ,令
,令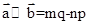 ,下面说法错误的是( )
,下面说法错误的是( )
A.若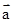 与 与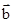 共线,则 共线,则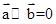 | B.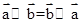 |
C.对任意的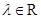 ,有 ,有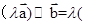 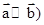 | D.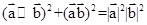 |
已知 ,
, ,点
,点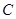 满足
满足 (
( ),且
),且 ,则
,则 等于
等于
A. | B.1 | C. | D. |
设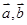 不共线,
不共线,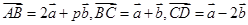 ,若
,若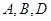 三点共线,则实数
三点共线,则实数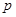 的值是: ( )
的值是: ( )
A.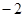 | B. | C.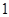 | D.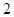 |
下列各组向量中,可以作为基底的是 ( )
A. | B.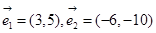 |
C.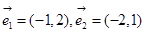 | D.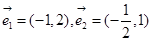 |
已知向量 ,
, 满足|
满足| |=2,|
|=2,| |=3,|2
|=3,|2 +
+ |=
|=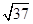 ,则
,则 与
与 的夹角为
的夹角为
| A.30° | B.45° | C.60° | D.90° |
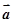 是已知的平面向量且
是已知的平面向量且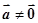 ,关于向量
,关于向量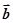 ,总存在向量
,总存在向量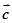 ,使
,使 ;
;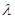 和
和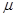 ,使
,使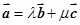 ;
;