题目内容
已知平面向量a、b,|a|=1,|b|=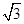 ,且|2a+b|=
,且|2a+b|=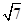 ,则向量a与向量a+b的夹角为( )
,则向量a与向量a+b的夹角为( )
A.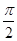 | B.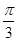 | C.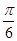 | D.π |
B
解析试题分析:
 ,结合平行四边形法则可知
,结合平行四边形法则可知 是以
是以 为临边的矩形的对角线向量,所以所求夹角
为临边的矩形的对角线向量,所以所求夹角 满足
满足
考点:向量的夹角及平行四边形法则
点评:设 夹角为
夹角为 ,则
,则 ,要求两向量的夹角需求出两向量的模及数量积,而后代入公式即可
,要求两向量的夹角需求出两向量的模及数量积,而后代入公式即可

练习册系列答案
相关题目
定义平面向量之间的一种运算“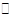 ”如下,对任意的
”如下,对任意的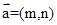 ,
,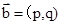 ,令
,令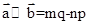 ,下面说法错误的是( )
,下面说法错误的是( )
A.若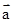 与 与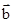 共线,则 共线,则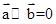 | B.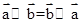 |
C.对任意的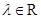 ,有 ,有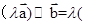 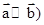 | D.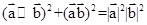 |
若向量 =(1,1),
=(1,1), =(2,5),
=(2,5),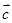 =(3,x),满足条件
=(3,x),满足条件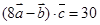 ,则x=( )
,则x=( )
| A.6 | B.5 | C.4 | D.3 |
已知向量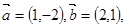 则与
则与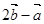 同方向的单位向量是( )
同方向的单位向量是( )
A.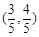 | B.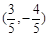 | C.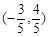 | D.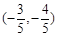 |
设向量 ,
,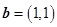 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. | C. 与 与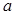 垂直 垂直 | D. ∥ ∥ |
已知向量 ,
, 满足|
满足| |=2,|
|=2,| |=3,|2
|=3,|2 +
+ |=
|=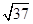 ,则
,则 与
与 的夹角为
的夹角为
| A.30° | B.45° | C.60° | D.90° |
已知 ,若向量
,若向量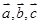 共面,
共面,
则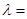 ( )
( )
A.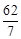 | B.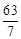 | C.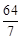 | D.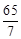 |
已知向量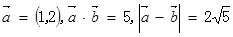 ,则
,则 等于( )
等于( )
A.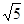 | B.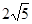 | C.25 | D.5 |
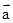 =(1,2),
=(1,2),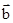 =(2,-3),若向量
=(2,-3),若向量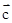 满足
满足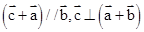 则向量c=( )
则向量c=( )