题目内容

根据下面一组等式

可得 S1+S3+S5+…+S2n-1=
 
．
考点：归纳推理
专题：规律型
分析：分别计算出S1，S1+S3，S1+S3+S5，S1+S3+S5+S7的值，然后利用归纳推理进行归纳即可．
解答： 解：由等式可知S1=1=14，
S1+S3=1+15=16=24，
S1+S3+S5=1+15+65=81=34，
S1+S3+S5+S7=81+175=256=44，
由归纳推理可知S1+S3+S5+…+S2n-1=n4，
故答案为：n4．
点评：本题主要考查归纳推理的应用，根据等式的特点找出规律是解决本题的关键．
练习册系列答案
相关题目
一个多面体的三视图分别为正方形、等腰三角形和矩形，如图所示．则该多面体的体积为
 
．
已知l1和l2是平面内互相垂直的两条直线，它们的交点为A，异于点A的两动点B、C分别在l1、l2上，且BC=3，则过A、B、C三点的动圆所形成的图形面积为（　　）
A、6π
B、9π
C、
9π
2
D、
9
4
π
已知
a
=(1，1)，
b
=(-1，1)，
m
=
a
-λ
b
，
n
=2
a
+
b
．
（1）若
m
∥
n
，求实数λ的值；
（2）若
m
⊥
n
，求实数λ的值．
已知一元二次不等式f（x）＜0的解集为{x|x＜-2或x＞2}，则f（10x）＞0的解集为
 
．
为了得到函数y=3(
1
3
)x的图象，可将函数y=(
1
3
)x的图象向
 
平移
 
个单位．
已知偶函数f（x）在区间[0，+∞）单调递减，则满足f（lnx）＞f（1）的x取值范围是（　　）
A、（
1
e
，1）
B、（0，
1
e
）∪（1，+∞）
C、（
1
e
，e）
D、（0，1）∪（e，+∞）
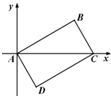如图，在平面直角坐标系中，已知平行四边形ABCD的三个顶点坐标：A（0，0），B（3，
3
），C（4，0）．
（1）求边CD所在直线的方程（结果写成一般式）；
（2）证明平行四边形ABCD为矩形，并求其面积．
已知直线ax+by+c=0（abc≠0）与圆x2+y2=1相切，若△ABC的三边长分别为|a|，|b|，|c|，则该三角形为
 
（判断三角形的形状）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网