Question

设不等式组

x+y-4≤0 x-y+4≥0 y≥0

表示的平面区域为M，不等式组

-t≤x≤t 0≤y≤4-t

（0≤t≤4）表示的平面区域为N．在M内随机取一个点，这个点在N内的概率为P．①当t=1时，P=

 

；②P的最大值是

 

．

Answer 1

考点：几何概型

专题：概率与统计

分析：分别求出对应区域的面积，利用几何概型的概率公式即可得到结论．

解答： 解：①不等式组

x+y-4≤0 x-y+4≥0 y≥0

表示的平面区域为M，则对应三角形的面积S_M=

1

2

×8×4=16．
不等式组

-t≤x≤t 0≤y≤4-t

（0≤t≤4）表示的平面区域为矩形，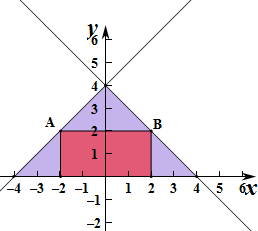
则对应的矩形面积为2t（4-t）=-2t²+8t=-2（t-2）²+8，
当t=1时，对应的面积S₁=2×3=6，此时对应的概率P=

6

16

=

3

8

．
②当t=2时，区域N的面积最大为8，此时区域N的最大面积为8，
则由几何概型的概率公式可知P的最大值是

8

16

=

1

2

，
故答案为：①

3

8

，②

1

2

．

点评：本题主要考查几何概型的概率计算，根据二次函数的性质求出区域N的最大值是解决本题的关键．