题目内容
17.由空间一点O出发的四条射线两两所成的角相等,则这个角的余弦值为-$\frac{1}{3}$.分析 构造正四面体ABCD中,中心O到各顶点连线所夹的角相等,则∠AOD就为所求的角,由此能求出这个角的余弦值.
解答 解:如图,正四面体ABCD中,中心O到各顶点连线所夹的角相等,
则∠AOD就为所求的角,
设正四面体ABCD的棱长为a,
作AE⊥面BCD,垂足为E,作BF⊥CD,交CD于F,则O∈AE,E∈AF,连结AF,
则BF=$\sqrt{{a}^{2}-(\frac{a}{2})^{2}}$=$\frac{\sqrt{3}}{2}a$,BE=$\frac{2}{3}BF=\frac{\sqrt{3}}{3}a$,AE=$\sqrt{{a}^{2}-(\frac{\sqrt{3}}{3}a)^{2}}$=$\frac{\sqrt{6}}{3}a$,
设OA=OB=r,则OE=$\frac{\sqrt{6}}{3}a-r$,
则${r}^{2}=(\frac{\sqrt{3}}{3}a)^{2}+(\frac{\sqrt{6}}{3}a-r)^{2}$,
解得r=$\frac{\sqrt{6}}{4}a$,
∴cos∠AOD=$\frac{O{A}^{2}+O{D}^{2}-A{D}^{2}}{2OA•OD}$=$\frac{\frac{3}{8}{a}^{2}+\frac{3}{8}{a}^{2}-{a}^{2}}{2×\frac{\sqrt{6}}{4}a×\frac{\sqrt{6}}{4}a}$=-$\frac{1}{3}$.
∴这个角的余弦值为-$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 本题考查角的余弦值的求法,是中档题,解题时要认真审题,注意构造法、余弦定理的合理运用.

练习册系列答案
相关题目
5.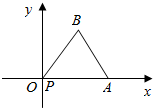 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )| A. | (-$\frac{37}{3}$,-9) | B. | (-∞,-$\frac{37}{3}$) | C. | (-$\frac{37}{3}$,-5) | D. | (-9,-5) |
12.设集合A={$\frac{n}{2}$|n∈Z},B={n|n∈Z},C={n+$\frac{1}{2}$|n∈Z},D={$\frac{n}{3}$+$\frac{1}{6}$|n∈Z},则在下列关系式中,成立的是( )
| A. | A$\underset{?}{≠}$B$\underset{?}{≠}$C$\underset{?}{≠}$D | B. | A∩B=∅,C∩D=∅ | C. | A=B∪C,C$\underset{?}{≠}$D | D. | A∪B=B ,C∩D=∅ |
2.定义在(0,π)上的函数f(π-x)=f(x),对任意x$∈(0,\frac{π}{2})$,不等式f(x)-f′(x)tanx>0恒成立,则下列不等式成立的是( )
| A. | $\sqrt{6}$f($\frac{π}{6}$)$<\sqrt{3}$f($\frac{π}{4}$)$<\sqrt{2}$f($\frac{2π}{3}$) | B. | $\sqrt{6}$f($\frac{π}{6}$)$<\sqrt{2}$f($\frac{2π}{3}$)$<\sqrt{3}$f($\frac{π}{4}$) | C. | $\sqrt{2}$f($\frac{2π}{3}$)$<\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{6}$f($\frac{π}{6}$) | D. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{6}$f($\frac{π}{6}$)$\sqrt{2}$f($\frac{2π}{3}$) |
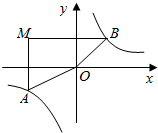 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.