题目内容
15.f(x)是定义在(-1,1)上的增函数,且f(x)+f(-x)=0,若f(1-a)+f(1-a2)>0,则a∈(0,1).分析 由条件利用函数的奇偶性、单调性和定义域,求得a的范围.
解答 解:由f(x)+f(-x)=0,可得f(-x)=-f(x),故f(x)为奇函数.
不等式f(1-a)+f(1-a2)>0,即 f(1-a)>f(a2-1).
再根据f(x)是定义在(-1,1)上的增函数,可得1>1-a>a2-1>-1,
即 $\left\{\begin{array}{l}{1>1-a}\\{1-a{>a}^{2}-1}\\{{a}^{2}-1>-1}\end{array}\right.$,求得0<a<1,
故答案为:(0,1).
点评 本题主要求函数的奇偶性、单调性和定义域,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
10.函数y=(a-2)x在R上为增函数,则a的取值范围是( )
| A. | a>3 | B. | a>0且a≠1 | C. | a<3 | D. | 2<a<3 |
5.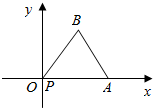 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )| A. | (-$\frac{37}{3}$,-9) | B. | (-∞,-$\frac{37}{3}$) | C. | (-$\frac{37}{3}$,-5) | D. | (-9,-5) |
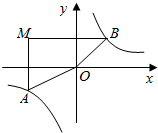 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.