题目内容
在△ABC中，若
=
，△ABC的形状为（ ）
| a2 |
| b2 |
| sinAcosB |
| cosAsinB |
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
考点：余弦定理
专题：解三角形
分析：已知等式左边利用正弦定理化简，整理后得到sin2A=sin2B，进而得到2A=2B或2A+2B=π，即可确定出三角形形状．
解答：
解：已知等式利用正弦定理
=
化简得：
=
=
，
整理得：
=
，即sinAcosA=sinBcosB，
∴2sinAcosA=2sinBcosB，即sin2A=sin2B，
∴2A=2B或2A+2B=π，即A=B或A+B=
，
则△ABC为等腰三角形或直角三角形．
故选：C．
| a |
| sinA |
| b |
| sinB |
| a2 |
| b2 |
| sin2A |
| sin2B |
| sinAcosB |
| cosAsinB |
整理得：
| sinA |
| sinB |
| cosB |
| cosA |
∴2sinAcosA=2sinBcosB，即sin2A=sin2B，
∴2A=2B或2A+2B=π，即A=B或A+B=
| π |
| 2 |
则△ABC为等腰三角形或直角三角形．
故选：C．
点评：此题考查了正弦定理，二倍角的正弦函数公式，熟练掌握正弦定理是解本题的关键．
练习册系列答案
相关题目
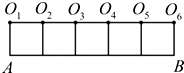如图，在5个并排的正方形图案中作出一个∠AOnB=135°（n=1，2，3，4，5，6），则n=（ ）| A、1，6 | B、2，5 |
| C、3，4 | D、2，3，4，5 |
等差数列{an}中，d=-3，a7=10，则a1等于（ ）
| A、-39 | B、28 | C、39 | D、32 |
已知数列{an}的前n项的是Sn=n2，则a6的值是（ ）
| A、9 | B、10 | C、11 | D、12 |
下列各对函数中，相同的是（ ）
A、f（x）=
| ||||||||
| B、f（x）=lgx2，g（x）=2lgx | ||||||||
C、f（x）=
| ||||||||
D、f（μ）=
|
sin15°cos75°-cos15°sin105°的值为（ ）
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
将角
表示为2kπ+α（k∈Z）的形式，则使|α|最小的角α是（ ）
| 19π |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
设集合M={1，2，3}，N={1，2}，则M∪N等于（ ）
| A、{1，2} |
| B、{1，3} |
| C、{2，3} |
| D、{1，2，3} |