题目内容
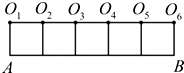 如图,在5个并排的正方形图案中作出一个∠AOnB=135°(n=1,2,3,4,5,6),则n=( )
如图,在5个并排的正方形图案中作出一个∠AOnB=135°(n=1,2,3,4,5,6),则n=( )| A、1,6 | B、2,5 |
| C、3,4 | D、2,3,4,5 |
考点:两角和与差的正切函数
专题:三角函数的求值
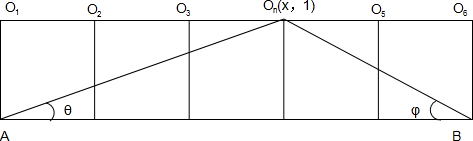
分析:设On(x,1),∠OnAB=θ,∠OnBA=φ,作出图形,利用两角和的正切可求得tan(θ+φ)=
=
=
=1,从而可得答案.
| tanθ+tanφ |
| 1-tanθtanφ |
| ||||
1-
|
| 5 |
| -x2+5x-1 |
解答:
解:设On(x,1),∠OnAB=θ,∠OnBA=φ,
则tanθ=
,tanφ=
,∵∠AOnB=135°,
∴θ+φ=
,
∴tan(θ+φ)=
=
=
=1,
解得:x=3或x=4,依题意,n=x,即n=3或n=4.
故选:C.

则tanθ=
| 1 |
| x |
| 1 |
| 5-x |
∴θ+φ=
| π |
| 4 |
∴tan(θ+φ)=
| tanθ+tanφ |
| 1-tanθtanφ |
| ||||
1-
|
| 5 |
| -x2+5x-1 |
解得:x=3或x=4,依题意,n=x,即n=3或n=4.
故选:C.
点评:本题考查两角和的正切,设On(x,1),∠OnAB=θ,∠OnBA=φ,求得tan(θ+φ)=
=1是关键,考查转化思想与运算求解能力,属于中档题.
| 5 |
| -x2+5x-1 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知log3m+log3n=2,则m+n的最小值是( )
A、2
| ||
| B、2 | ||
| C、6 | ||
D、3
|
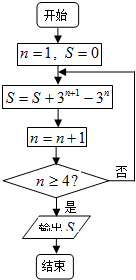
某程序的框图如图所示,则运行该程序后输出的B的值是( )


| A、63 | B、31 | C、15 | D、7 |
有一种彩票头奖的中奖概率是一千万分之一,若买五注不同号码,中奖概率是( )
| A、千万分之一 |
| B、千万分之五 |
| C、千万分之十 |
| D、千万分之二十 |
某工厂年产量第一年增长率为a,第二年增长率为b,则这两年平均增长率x满足( )
A、x=
| ||
B、x≤
| ||
C、x<
| ||
D、x≥
|
在△ABC中,若
=
,△ABC的形状为( )
| a2 |
| b2 |
| sinAcosB |
| cosAsinB |
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |