题目内容
已知角α的终边经过点P(-4,3).
(1)求
的值;
(2)求cos(α+
)的值.
(1)求
| sin(π-α)+cos(-α) |
| tan(π+α) |
(2)求cos(α+
| π |
| 6 |
考点:三角函数中的恒等变换应用,任意角的三角函数的定义
专题:计算题,三角函数的求值
分析:根据三角函数的定义求出角α的正弦、余弦和正切值,(1)利用诱导公式化简,然后代入;(2)利用两角和的余弦公式展开,然后代入.
解答:
解:∵角α的终边经过点P(-4,3),
∴r=
=5
∴sinα=
,cosα=-
,tanα=-
,
(1)
=
=
=
(2)cos(α+
)=
cosα-
sinα
=
×(-
)-
×
=-
.
∴r=
| (-4)2+32 |
∴sinα=
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
(1)
| sin(π-α)+cos(-α) |
| tan(π+α) |
=
| sinα+cosα |
| tanα |
=
| ||||
-
|
=
| 4 |
| 15 |
(2)cos(α+
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
=-
4
| ||
| 10 |
点评:本题考查了三角函数的定义、诱导公式和两角和的余弦公式,解决本题的关键是根据三角函数的定义求出角α的各种三角函数值,利用公式化简时要注意判断符号.

练习册系列答案
相关题目
在△ABC中,若
=
,△ABC的形状为( )
| a2 |
| b2 |
| sinAcosB |
| cosAsinB |
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
设数列{an}中,a1=2,an+1=an+n+1,数列{bn}满足bn=
(n∈N*),则数列{bn}的前n项和为( )
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
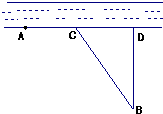 在甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在他们之间的此岸边合建一个污水处理厂C,从污水处理厂到甲厂和乙厂的铺设的排污管道费用分别为每千米3a元和5a元,记铺设管道的总费用为y元.
在甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在他们之间的此岸边合建一个污水处理厂C,从污水处理厂到甲厂和乙厂的铺设的排污管道费用分别为每千米3a元和5a元,记铺设管道的总费用为y元.