题目内容
已知函数f(x)=sin(x+θ)+acos(x+2θ),其中a∈R,θ∈(-
,
)
(1)当a=
,θ=
时,求f(x)在区间[0,π]上的最大值与最小值;
(2)若f(
)=0,f(π)=1,求a,θ的值.
| π |
| 2 |
| π |
| 2 |
(1)当a=
| 2 |
| π |
| 4 |
(2)若f(
| π |
| 2 |
考点:两角和与差的正弦函数,两角和与差的余弦函数,正弦函数的定义域和值域
专题:三角函数的求值
分析:(1)由条件利用两角和差的正弦公式、余弦公式化简函数的解析式为f(x)=-sin(x-
),再根据x∈[0,π],利用正弦函数的定义域和值域求得函数的最值.
(2)由条件可得θ∈(-
,
),cosθ-asin2θ=0 ①,-sinθ-acos2θ=1 ②,由这两个式子求出a和θ的值.
| π |
| 4 |
(2)由条件可得θ∈(-
| π |
| 2 |
| π |
| 2 |
解答:
解:(1)当a=
,θ=
时,f(x)=sin(x+θ)+acos(x+2θ)
=sin(x+
)+
cos(x+
)=
sinx+
cosx-
sinx=-
sinx+
cosx
=sin(
-x)=-sin(x-
).
∵x∈[0,π],∴x-
∈[-
,
],
∴sin(x-
)∈[-
,1],
∴-sin(x-
)∈[-1,
],
故f(x)在区间[0,π]上的最小值为-1,最大值为
.
(2)∵f(x)=sin(x+θ)+acos(x+2θ),a∈R,θ∈(-
,
),
f(
)=0,f(π)=1,
∴cosθ-asin2θ=0 ①,-sinθ-acos2θ=1 ②,
由①求得sinθ=
,由②可得cos2θ=
=-
-
.
再根据cos2θ=1-2sin2θ,可得-
-
=1-2×
,
求得 a=-1,∴sinθ=-
,θ=-
.
综上可得,所求的a=-1,θ=-
.
| 2 |
| π |
| 4 |
=sin(x+
| π |
| 4 |
| 2 |
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
=sin(
| π |
| 4 |
| π |
| 4 |
∵x∈[0,π],∴x-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴sin(x-
| π |
| 4 |
| ||
| 2 |
∴-sin(x-
| π |
| 4 |
| ||
| 2 |
故f(x)在区间[0,π]上的最小值为-1,最大值为
| ||
| 2 |
(2)∵f(x)=sin(x+θ)+acos(x+2θ),a∈R,θ∈(-
| π |
| 2 |
| π |
| 2 |
f(
| π |
| 2 |
∴cosθ-asin2θ=0 ①,-sinθ-acos2θ=1 ②,
由①求得sinθ=
| 1 |
| 2a |
| 1+sinθ |
| -a |
| 1 |
| a |
| 1 |
| 2a2 |
再根据cos2θ=1-2sin2θ,可得-
| 1 |
| a |
| 1 |
| 2a2 |
| 1 |
| 4a2 |
求得 a=-1,∴sinθ=-
| 1 |
| 2 |
| π |
| 6 |
综上可得,所求的a=-1,θ=-
| π |
| 6 |
点评:本题主要考查两角和差的正弦公式、余弦公式,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
. |
| z |
. |
| z |
. |
| z |
| A、1+i | B、-1-i |
| C、-1+i | D、1-i |
 如图,点A为圆外一点,过点A作圆的两条切线,切点分别为B,C,ADE是圆的割线,连接CD,BD,BE,CE.
如图,点A为圆外一点,过点A作圆的两条切线,切点分别为B,C,ADE是圆的割线,连接CD,BD,BE,CE.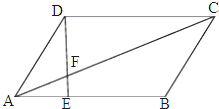 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则