题目内容
某超市制定了一份“周日”促销活动方案,当天单张购物发票数额不低于100元的顾客可参加“摸球抽奖赢代金券”活动,规则如下:
①单张购物发票每满100元允许摸出一个小球,最多允许摸出三个小球(例如,若顾客购买了单张发票数额230元的商品,则需摸出两个小球);
②每位参加抽奖的顾客要求从装有1个红球,2个黄球,3个白球的箱子中一次性摸出允许摸出的所有小球;
③摸出一个红球获取25元代金券,摸出一个黄球获取15元代金券,摸出一个白球获取5元代金券.
已知活动当日小明购买了单张发票数额为338元商品,求小明参加抽奖活动时:
(Ⅰ)小明摸出的球中恰有两个是黄球的概率;
(Ⅱ)小明获得代金券不低于30元的概率.
①单张购物发票每满100元允许摸出一个小球,最多允许摸出三个小球(例如,若顾客购买了单张发票数额230元的商品,则需摸出两个小球);
②每位参加抽奖的顾客要求从装有1个红球,2个黄球,3个白球的箱子中一次性摸出允许摸出的所有小球;
③摸出一个红球获取25元代金券,摸出一个黄球获取15元代金券,摸出一个白球获取5元代金券.
已知活动当日小明购买了单张发票数额为338元商品,求小明参加抽奖活动时:
(Ⅰ)小明摸出的球中恰有两个是黄球的概率;
(Ⅱ)小明获得代金券不低于30元的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)小明一次性购买了338元商品,可以一次摸三个球,所有情况有:
=20;小明摸出的球中恰有两个是黄球的情况有4种,代入古典概型概率公式即可;
(Ⅱ)设小明获得代金券不低于30元为事件B,
包含两种情况,列举出
包含的基本事件个数,代入古典概型概率公式求出
的概率,代入对立事件概率公式求出即可.
| C | 3 6 |
(Ⅱ)设小明获得代金券不低于30元为事件B,
. |
| B |
. |
| B |
. |
| B |
解答:
解:解:(Ⅰ)用“a“代表红球,“b1,b2“代表两个黄球,“c1,c2 ,c3“代表三个白球,
∵小明一次性购买了338元商品,
∴可以一次摸三个球,所有情况有:
=20;
小明摸出的球中恰有两个是黄球的情况有4种,
∴小明摸出的球中恰有两个是黄球的概率为P=
=
;
(Ⅱ)设小明获得代金券不低于30元为事件B,
包含两种情况,
一种是摸出三个球都是白球,基本事件为c1c2c3,基本事件个数为1;
另一种是摸出一个黄球两个白球,基本事件为b1c1c2,b1c1c3,b1c2c3,b2c1c2,b2c1c3,b2c2c3,基本事件是6,
∴P(
)=
∴P(B)=1-P(
)=
∵小明一次性购买了338元商品,
∴可以一次摸三个球,所有情况有:
| C | 3 6 |
小明摸出的球中恰有两个是黄球的情况有4种,
∴小明摸出的球中恰有两个是黄球的概率为P=
| 4 |
| 20 |
| 1 |
| 5 |
(Ⅱ)设小明获得代金券不低于30元为事件B,
. |
| B |
一种是摸出三个球都是白球,基本事件为c1c2c3,基本事件个数为1;
另一种是摸出一个黄球两个白球,基本事件为b1c1c2,b1c1c3,b1c2c3,b2c1c2,b2c1c3,b2c2c3,基本事件是6,
∴P(
. |
| B |
| 7 |
| 20 |
∴P(B)=1-P(
. |
| B |
| 13 |
| 20 |
点评:本题考查古典概型的概率公式;考查求事件的基本事件个数常用列举法和排列组合,属于一道基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
| A、f(x)g(x)是偶函数 |
| B、|f(x)|g(x)是奇函数 |
| C、f(x)|g(x)|是奇函数 |
| D、|f(x)g(x)|是奇函数 |
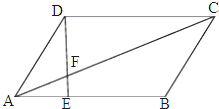 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则