题目内容
在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程ρ=2cosθ,θ∈[0,
].
(Ⅰ)求C的参数方程;
(Ⅱ)设点D在C上,C在D处的切线与直线l:y=
x+2垂直,根据(Ⅰ)中你得到的参数方程,确定D的坐标.
| π |
| 2 |
(Ⅰ)求C的参数方程;
(Ⅱ)设点D在C上,C在D处的切线与直线l:y=
| 3 |
考点:参数方程化成普通方程,利用导数研究曲线上某点切线方程,圆的参数方程
专题:坐标系和参数方程
分析:(Ⅰ)半圆C的极坐标方程化为直角坐标方程为 (x-1)2+y2=1,令x-1=cosα∈[-1,1],y=sinα,可得半圆C的参数方程.
(Ⅱ)由题意可得直线CD和直线l平行.设点D的坐标为(1+cosα,sinα),根据直线CD和直线l的斜率相等求得 cotα 的值,可得α 的值,从而得到点D的坐标.
(Ⅱ)由题意可得直线CD和直线l平行.设点D的坐标为(1+cosα,sinα),根据直线CD和直线l的斜率相等求得 cotα 的值,可得α 的值,从而得到点D的坐标.
解答:
解:(Ⅰ)半圆C的极坐标方程ρ=2cosθ,θ∈[0,
],即 ρ2=2ρcosθ,
化为直角坐标方程为 (x-1)2+y2=1,x∈[0,2]、y∈[0,1].
令x-1=cosα∈[-1,1],y=sinα,α∈[0,π].
故半圆C的参数方程为
,α∈[0,π].
(Ⅱ)由于点D在C上,半圆C在D处的切线与直线l:y=
x+2垂直,
∴直线CD和直线l平行,故直线CD和直线l斜率相等.
设点D的坐标为(1+cosα,sinα),∵C(1,0),∴
=
,
解得tanα=
,即α=
,
故点D的坐标为(
,
).
| π |
| 2 |
化为直角坐标方程为 (x-1)2+y2=1,x∈[0,2]、y∈[0,1].
令x-1=cosα∈[-1,1],y=sinα,α∈[0,π].
故半圆C的参数方程为
|
(Ⅱ)由于点D在C上,半圆C在D处的切线与直线l:y=
| 3 |
∴直线CD和直线l平行,故直线CD和直线l斜率相等.
设点D的坐标为(1+cosα,sinα),∵C(1,0),∴
| sinα-0 |
| (1+cosα)-1 |
| 3 |
解得tanα=
| 3 |
| π |
| 3 |
故点D的坐标为(
| 3 |
| 2 |
| ||
| 2 |
点评:本题主要考查把极坐标方程化为直角坐标方程,把直角坐标方程化为参数方程,注意参数的范围,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
下列函数为偶函数的是( )
| A、f(x)=x-1 |
| B、f(x)=x2+x |
| C、f(x)=2x-2-x |
| D、f(x)=2x+2-x |
 如图,点A为圆外一点,过点A作圆的两条切线,切点分别为B,C,ADE是圆的割线,连接CD,BD,BE,CE.
如图,点A为圆外一点,过点A作圆的两条切线,切点分别为B,C,ADE是圆的割线,连接CD,BD,BE,CE.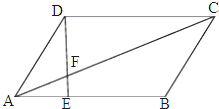 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则 如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=
如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=
 幂函数y=xa,当a取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图),设点A(1,0)、B(0,1),若y=xα,y=xβ的图象与线段AB分别交于M、N,且
幂函数y=xa,当a取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图),设点A(1,0)、B(0,1),若y=xα,y=xβ的图象与线段AB分别交于M、N,且