题目内容
2.已知f(α)=$\frac{sin(α-π)cos(\frac{3π}{2}+α)tan(-α-π)}{sin(5π+α)ta{n}^{2}(-α-2π)}$(1)化简f(α);
(2)若α是第三象限角,且cos($α+\frac{π}{2}$)=$\frac{1}{5}$,求f(α)的值;
(3)若$α=\frac{2015}{3}π$,求f(α)的值.
分析 (1)直接利用诱导公式化简求值;
(2)由cos($α+\frac{π}{2}$)=$\frac{1}{5}$,求得cosα的值,则f(α)的值可求;
(3)把$α=\frac{2015}{3}π$代入f(α),利用诱导公式化简求值.
解答 解:(1)f(α)=$\frac{sin(α-π)cos(\frac{3π}{2}+α)tan(-α-π)}{sin(5π+α)ta{n}^{2}(-α-2π)}$
=$\frac{-sinα•sinα•(-tanα)}{-sinα•ta{n}^{2}α}$=-cosα;
(2)∵α是第三象限角,且cos($α+\frac{π}{2}$)=$\frac{1}{5}$,
∴-sin$α=\frac{1}{5}$,sin$α=-\frac{1}{5}$,
∵α是第三象限角,∴cosα=$-\sqrt{1-(-\frac{1}{5})^{2}}=-\frac{2\sqrt{6}}{5}$,
则f(α)=-cosα=$\frac{2\sqrt{6}}{5}$;
(3)∵$α=\frac{2015}{3}π$,
∴f(α)=-cos$\frac{2015}{3}π$=-cos(671π+$\frac{2π}{3}$)=cos$\frac{2π}{3}$=$-\frac{1}{2}$.
点评 本题考查了诱导公式应用,考查了三角函数的化简求值,是中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
12.设x∈R,则“1-x-2x2<0”是“|2-x|<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
10.甲、乙、丙3名教师安排在10月1日至5日的5天中值班,要求每人值班一天且每天至多安排一人.其中甲不在10月1日值班且丙不在10月5日值班,则不同的安排方法有( )种.
| A. | 36 | B. | 39 | C. | 42 | D. | 45 |
17.设集合A={4,5,6,9},B={3,4,6,8,9},全集U=A∪B,则集合∁U(A∩B)的元素个数共有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
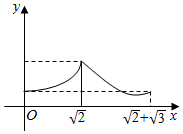
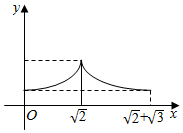
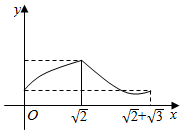
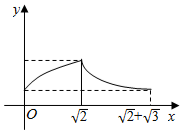
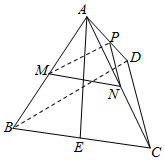 如图,在正三棱锥A-BCD中,M,N,E分别为AB,AC,BC边的中点,侧棱长为$\sqrt{2}$,且三条棱两两垂直,点P由A向E沿A→D→E运动,设点P运动的路程为x,△PMN的面积为y,则函数y=f(x)的图象大致是( )
如图,在正三棱锥A-BCD中,M,N,E分别为AB,AC,BC边的中点,侧棱长为$\sqrt{2}$,且三条棱两两垂直,点P由A向E沿A→D→E运动,设点P运动的路程为x,△PMN的面积为y,则函数y=f(x)的图象大致是( )