题目内容
14．设函数f（x），g（x）在区间（0，5）内导数存在，且有以下数据：| x | 1 | 2 | 3 | 4 |
| f（x） | 2 | 3 | 4 | 1 |
| f′（x） | 3 | 4 | 2 | 1 |
| g（x） | 3 | 1 | 4 | 2 |
| g′（x） | 2 | 4 | 1 | 3 |
分析 求出f′（1）=3，f（1）=2，即可求出曲线f（x）在点（1，f（1））处的切线方程．利用复合函数的导数公式，可得函数f（g（x））在x=2处的导数值，
解答 解：f′（1）=3，f（1）=2，∴曲线f（x）在点（1，f（1））处的切线方程是y=3x-1，
[f（g（x））]′=f′（g（x））g′（x），x=2时，f′（g（2））g′（2）=3×4=12，
故答案为y=3x-1；12
点评 本题考查导数的计算，考查导数的几何意义，属于中档题．
练习册系列答案
发散思维新课堂系列答案
相关题目
9．
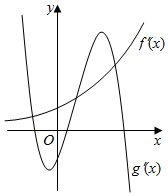定义在R上的函数f（x）和g（x），其各自导函数f′（x）f和g′（x）的图象如图所示，则函数F（x）=f（x）-g（x）极值点的情况是（ ）
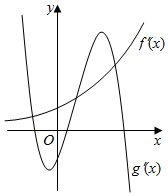定义在R上的函数f（x）和g（x），其各自导函数f′（x）f和g′（x）的图象如图所示，则函数F（x）=f（x）-g（x）极值点的情况是（ ）| A． | 只有三个极大值点，无极小值点 | B． | 有两个极大值点，一个极小值点 | ||
| C． | 有一个极大值点，两个极小值点 | D． | 无极大值点，只有三个极小值点 |
19．下列各数中，是纯虚数的是（ ）
| A． | i2 | B． | π | C． | 1+$\sqrt{3}$i | D． | （1+$\sqrt{3}$）i |