题目内容
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F、G分别为PC、PD、BC的中点.
(1)求证:PA⊥EF;
(2)求二面角D-FG-E的余弦值.
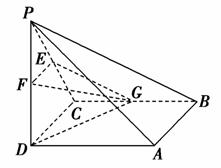
以D为坐标原点,建立如图所示的空间直角坐标系D-xyz,则D(0,0,0),A(0,2,0),C(-2,0,0),P(0,0,2),E(-1,0,1),F(0,0,1),G(-2,1,0).
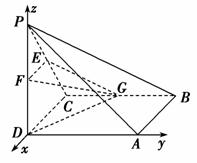
(1)证明:由于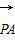 =(0,2,-2),
=(0,2,-2),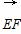 =(1,0,0),
=(1,0,0),
则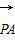 ·
·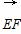 =1×0+0×2+(-2)×0=0,
=1×0+0×2+(-2)×0=0,
∴PA⊥EF.
(2)易知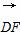 =(0,0,1),
=(0,0,1),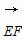 =(1,0,0),
=(1,0,0),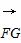 =(-2,1,-1),
=(-2,1,-1),
设平面DFG的法向量m=(x1,y1,z1),
则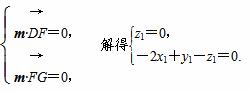
令x1=1,得m=(1,2,0)是平面DFG的一个法向量.
设平面EFG的法向量n=(x2,y2,z2),
同理可得n=(0,1,1)是平面EFG的一个法向量.
∵cos〈m,n〉=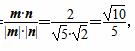
设二面角D-FG-E的平面角为θ,由图可知θ=π-〈m,n〉,∴cosθ=-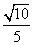 ,
,
∴二面角D-FG-E的余弦值为-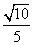 .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
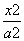 +
+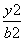 =1上的任意一点,F1、F2是它的两个焦点,O为坐标原点,
=1上的任意一点,F1、F2是它的两个焦点,O为坐标原点, 则动点Q的轨迹方程是________.
则动点Q的轨迹方程是________. B.
B.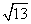 C.2
C.2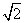 D.2
D.2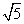
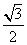 B.
B.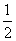
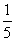 D.
D.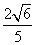
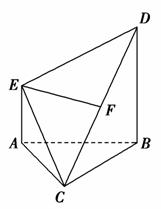
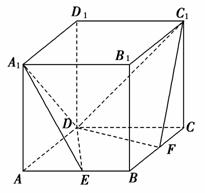
 ,AA′=1,点M、N分别为A′B和B′C′的中点.
,AA′=1,点M、N分别为A′B和B′C′的中点.
 Sh,其中S为底面面积,h为高).
Sh,其中S为底面面积,h为高).