题目内容
已知函数f(x)是定义在R的奇函数,当x≤0时,f(x)=x2,若对任意的x∈[t,t+1],不等式f(x)≤9f(x+t)恒成立,则实数t的最大值为( )
A、-
| ||
B、-
| ||
C、-
| ||
| D、2 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:根据函数的奇偶性的性质求出函数f(x)的表达式,并判断函数的单调性,利用函数的单调性将不等式恒成立进行转化,即可求出t的最大值.
解答:
解:若x>0,则-x<0,
∵当x≤0时,f(x)=x2,
∴f(-x)=x2,
∵f(x)是定义在R的奇函数,
∴f(-x)=x2=-f(x),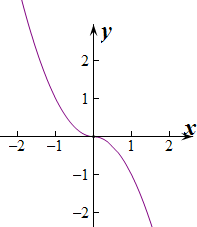
即f(x)=-x2,x>0,
即f(x)=
,
则函数f(x)的图象如图:
则函数f(x)在R上单调递减,
∵9f(x+t)=32f(x+t)=f(3x+3t),
∴对任意的x∈[t,t+1],不等式f(x)≤9f(x+t)恒成立,
等价为对任意的x∈[t,t+1],不等式f(x)≤f(3x+3t)恒成立,
即x≥3x+3t,即x≤-
t恒成立,
∵x∈[t,t+1],
∴t+1≤-
t恒成立,
即
t≤-1,解≥t≤-
,
则实数t的最大值为-
,
故选:A
∵当x≤0时,f(x)=x2,
∴f(-x)=x2,
∵f(x)是定义在R的奇函数,
∴f(-x)=x2=-f(x),
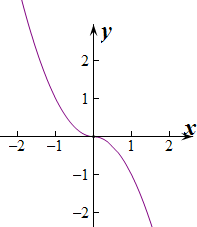
即f(x)=-x2,x>0,
即f(x)=
|
则函数f(x)的图象如图:
则函数f(x)在R上单调递减,
∵9f(x+t)=32f(x+t)=f(3x+3t),
∴对任意的x∈[t,t+1],不等式f(x)≤9f(x+t)恒成立,
等价为对任意的x∈[t,t+1],不等式f(x)≤f(3x+3t)恒成立,
即x≥3x+3t,即x≤-
| 3 |
| 2 |
∵x∈[t,t+1],
∴t+1≤-
| 3 |
| 2 |
即
| 5 |
| 2 |
| 2 |
| 5 |
则实数t的最大值为-
| 2 |
| 5 |
故选:A
点评:本题主要考查不等式恒成立问题,利用函数的奇偶性求出函数的表达式以及判断函数的单调性是解决本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
设复数z满足iz=1+2i,则z=( )
| A、2-i | B、-2-i |
| C、-2+i | D、2+i |
 某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.
某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.| A、11 | B、13 | C、15 | D、17 |
下列语句能使变量a的值为4的是( )
| A、INPUT a=4 |
| B、b=4,b=a |
| C、a=3,a=a+1 |
| D、2a=a+4 |
设p:“x,y,z中至少有一个等于1”?“(x-1)(y-1)(z-1)=0”;q:“
+|y-2|+(z-3)2=0”?“(x-1)(y-2)(z-3)=0”,那么p,q的真假是( )
| x-1 |
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x-y+3=0平行,若数列{
}的前n项和为Sn,则S2011的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
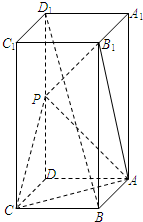 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=2AB,且点P为DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=2AB,且点P为DD1的中点. 在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C:
在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C: