题目内容
以M(-4,3)为圆心的圆与直线2x+y-5=0相离,那么圆M的半径r的取值范围是( )
| A、0<r<2 | ||
B、0<r<
| ||
C、0<r<2
| ||
| D、0<r<10 |
考点:直线与圆的位置关系
专题:直线与圆
分析:M(-4,3)到直线2x+y-5=0的距离d=
=2,由此能求出圆M的半径r的取值范围.
| |-8+3-5| | ||
|
解答:
解:∵以M(-4,3)为圆心的圆与直线2x+y-5=0相离,
M(-4,3)到直线2x+y-5=0的距离d=
=2,
∴0<r<2.
故选:A.
M(-4,3)到直线2x+y-5=0的距离d=
| |-8+3-5| | ||
|
∴0<r<2.
故选:A.
点评:本题考查圆的取值范围的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
方程x2=cosx的实根的个数是( )
| A、0 | B、1 | C、2 | D、3 |
集合M={x|x=
+
,k∈A},集合N={x|x=
+
,k∈z},则( )?
| k |
| 2 |
| 1 |
| 4 |
| k |
| 4 |
| 1 |
| 2 |
| A、M=N | B、M≠N |
| C、M≠N | D、M?N |
函数f(x)=
的图象大致为( )
| 1 |
| ln(x+1)-x |
A、 |
B、 |
C、 |
D、 |
设全集U=R,A={x|-3<x<0},B={x|x<-1},则图中阴影部分表示的集合为( )
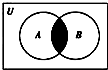

| A、(-3,-1) |
| B、(-1,0) |
| C、[-1,0) |
| D、(-∞,-1) |
使圆x2+y2=r2与x2+y2+2x-4y+4=0有交点的充要条件是( )
A、r<
| ||
B、r>
| ||
C、|r-
| ||
D、|r-
|
点P(tan2012°,cos2012°)位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合A={x||x|<2},B={x|
<2x<8},则A∩B=( )
| 1 |
| 2 |
| A、{x|-1<x<2} |
| B、{x|-1<x<3} |
| C、{x|-2<x<3} |
| D、{x|-2<x<2} |