题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,向量
=(-cosBcosC,1),
=(1,sinBsinC-
),且
⊥
.
(1)求cosB+sinC的取值范围;
(2)先给出下列三个条件:①a=1,②2c-(
+1)b=0,③B=
,试从中选择两个条件确定△ABC,并求出所确定的△ABC的面积.
| m |
| n |
| ||
| 2 |
| m |
| n |
(1)求cosB+sinC的取值范围;
(2)先给出下列三个条件:①a=1,②2c-(
| 3 |
| π |
| 4 |
考点:平面向量数量积的运算,正弦定理
专题:计算题,解三角形,平面向量及应用
分析:(1)利用
•
=0,推出cos(B+C)=-
,然后求出A=30°;
(2)方案一:选择①②,可以确定△ABC,通过余弦定理,得c=
,求出S△ABC;
方案二:选择①③,可以确定△ABC,由正弦定理的c,然后求出S△ABC.
| m |
| n |
| ||
| 2 |
(2)方案一:选择①②,可以确定△ABC,通过余弦定理,得c=
| ||||
| 2 |
方案二:选择①③,可以确定△ABC,由正弦定理的c,然后求出S△ABC.
解答:
解:(1)因为向量
=(-cosBcosC,1),
=(1,sinBsinC-
),且
⊥
,
所以-cosBcosC+sinBsinC-
=0,
所以cos(B+C)=-
,
因为A+B+C=π,所以cos(B+C)=-cosA,
所以cosA=
,A=30°.
(2)方案一:选择①②,可以确定△ABC,
因为A=30°,a=1,2c-(
+1)b=0,
由余弦定理,得:12=b2+(
b)2-2b•
b•
,
整理得:b2=2,b=
,c=
,
所以S△ABC=
bcsinA=
×
×
×
=
.
方案二:选择①③,可以确定△ABC,
因为A=30°,a=1,B=45°,C=105°,
又sin105°=sin(45°+60°)=sin45°cos60°+sin60°cos45°=
.
由正弦定理的c=
=
=
,
所以S△ABC=
acsinB=
×1×
×
=
.
| m |
| n |
| ||
| 2 |
| m |
| n |
所以-cosBcosC+sinBsinC-
| ||
| 2 |
所以cos(B+C)=-
| ||
| 2 |
因为A+B+C=π,所以cos(B+C)=-cosA,
所以cosA=
| ||
| 2 |
(2)方案一:选择①②,可以确定△ABC,
因为A=30°,a=1,2c-(
| 3 |
由余弦定理,得:12=b2+(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
整理得:b2=2,b=
| 2 |
| ||||
| 2 |
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
方案二:选择①③,可以确定△ABC,
因为A=30°,a=1,B=45°,C=105°,
又sin105°=sin(45°+60°)=sin45°cos60°+sin60°cos45°=
| ||||
| 4 |
由正弦定理的c=
| asinC |
| sinA |
| 1×sin105° |
| sin30° |
| ||||
| 2 |
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:本题考查向量的垂直,正弦定理的应用,考查分析问题解决问题的能力.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
阅读程序框图,如果输出i=5,那么在空白矩形框中填入的语句为( )


| A、S=2*i |
| B、S=2*i-1 |
| C、S=2*i-2 |
| D、S=2*i+4 |
已知向量
=(-3,4),则下列能使
=λ
+μ
(λ、μ∈R)成立的一组向量
,
是( )
| a |
| a |
| e1 |
| e2 |
| e1 |
| e2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知命题p:?x0∈R,x0-2>lgx0,命题q:?x∈(0,
),sinx+
≥2,则( )
| π |
| 2 |
| 1 |
| sinx |
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∧(¬q)是真命题 |
| D、命题p∨(¬q)是假命题 |
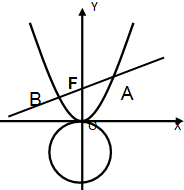 已知抛物线C:x2=4y,过焦点F的直线l与抛物线交于A,B两点(A在第一象限).
已知抛物线C:x2=4y,过焦点F的直线l与抛物线交于A,B两点(A在第一象限).