题目内容
9.在平面直角坐标系xOy中,设A,B分别为曲线y=$\sqrt{1{-x}^{2}}$与x轴的两个交点,C、D分别为曲线上的两个动点,则$\overrightarrow{AC}•\overrightarrow{BD}$的取值范围是[-4,$\frac{1}{2}$].分析 由向量的几何意义,以及直线和圆的位置关系即可求出.
解答 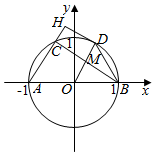 解:曲线y=$\sqrt{1{-x}^{2}}$为半圆,如图所示:A(-1,0),B(1,0),
解:曲线y=$\sqrt{1{-x}^{2}}$为半圆,如图所示:A(-1,0),B(1,0),
当$\overrightarrow{AC}$,$\overrightarrow{BD}$方向相反时,且长度均为2时,$\overrightarrow{AC}•\overrightarrow{BD}$=-4,
设D在$\overrightarrow{AC}$上的投影点为H,OD与BC的交于点M,OM=x,
则当DH为圆0的切线时,$\overrightarrow{AC}•\overrightarrow{BD}$=|$\overrightarrow{AC}$|•|$\overrightarrow{CH}$|=2x(1-x)≤$\frac{1}{2}$,(当且仅当x=$\frac{1}{2}$时等号成立)
所以则$\overrightarrow{AC}•\overrightarrow{BD}$的取值范围是[-4,$\frac{1}{2}$]
点评 本题考查了向量的几何意义,关键是掌握点位置关系,以及直线和圆的位置关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知函数f(x)=sin(ωx+φ)+$\frac{1}{2}$(ω≥0,|φ|<π)的图象与直线y=c($\frac{1}{2}$<c<$\frac{3}{2}$)的三个相邻交点的横坐标为2,6,18,若a=f(lg$\frac{1}{2}$),b=f(lg2),则以下关系式正确的是( )
| A. | a+b=0 | B. | a-b=0 | C. | a+b=1 | D. | a-b=1 |
17.函数y=ln|x|的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
1.与不等式log2x2<3同解的不等式是( )
| A. | log2x$<\frac{3}{2}$ | B. | x2<8 | C. | x2(x2-8)<0 | D. | ${log}_{\frac{1}{2}}$x2>3 |