题目内容
5.设{an}是公比大于1的等比数列,Sn为其前n项和,已知S3=7,a1+3,3a2,a3+4构成等差数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=an+lnan,求数列{bn}的前n项和Tn.
分析 (Ⅰ)根据题意,列出关于{an}的首项与公差的方程组,求出首项、公差代入通项公式即得数列{an}的通项公式.
(Ⅱ)将${a_n}={2^{n-1}}$代入bn,得到${b_n}={2^{n-1}}+(n-1)ln2$,利用分组法求出Tn.
解答 解:(Ⅰ)设数列{an}的公比为q(q>1),
由已知,得$\left\{\begin{array}{l}{a_1}+{a_2}+{a_3}=7\\ \frac{{({a_1}+3)+({a_3}+4)}}{2}=3{a_2}\end{array}\right.$可得$\left\{\begin{array}{l}{a_1}(1+q+{q^2})=7\\{a_1}(1-6q+{q^2})=-7\end{array}\right.$
解得$\left\{\begin{array}{l}{a_1}=1\\ q=2\end{array}\right.$,
故数列{an}的通项公式为${a_n}={2^{n-1}}$.
(Ⅱ)由(Ⅰ)得${b_n}={2^{n-1}}+(n-1)ln2$,
所以${T_n}=(1+2+{2^2}+…+{2^{n-1}})+[0+1+2+…+(n-1)]ln2$
=$\frac{{1-{2^n}}}{1-2}+\frac{n(n-1)}{2}ln2$
=${2^n}-1+\frac{n(n-1)}{2}ln2$.
点评 本题主要考查数列通项公式和前n项和的求解,利用分组求和法是解决本题的关键.

练习册系列答案
相关题目
15.设m,n是两条不同的直线,α,β是两个不同的平面,则m∥n 的一个充分不必要条件是( )
| A. | m⊥α,n⊥β,α∥β | B. | m∥α,n∥β,α∥β | C. | m∥α,n⊥β,α⊥β | D. | m⊥α,n⊥β,α⊥β |
16.若复数z满足(2-i)z=1-i(i为虚数单位),则复数z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.设集合U={1,2,3,4,5},集合A={x∈Z|x2-5x+4<0},集合B={1,2},则(∁UA)∩B=( )
| A. | {1} | B. | {1,2} | C. | {1,3} | D. | {2,3} |
20.已知函数f(x)=cos(2x-φ)-$\sqrt{3}$sin(2x-φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后关于y轴对称,则f(x)在区间$[{-\frac{π}{2},0}]$上的最小值为( )
| A. | -1 | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | -2 |
14.某产品的广告费用x与销售额y的统计数据如表:
用最小二乘法算得的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\widehat{b}$为7,据此预测广告费用为6万元时销售额为( )
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 32 | 35 | 45 | 52 |
| A. | 58.5万元 | B. | 77.5万元 | C. | 59万元 | D. | 70万元 |
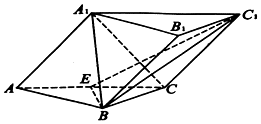 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.