题目内容
已知数列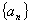 中,
中,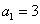 ,满足
,满足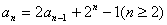 。
。
(1)求证:数列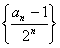 为等差数列;
为等差数列;
(2)求数列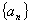 的前
的前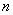 项和
项和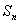 .
.
(1)用定义证明 (2)
解析试题分析:(1)证明:由定义
故 是以
是以 为首项,1为公差的等差数列。
为首项,1为公差的等差数列。
(2)由(1)知

令 的前
的前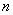 项和,则
项和,则 ①
① ②
②
①-②得
 故
故
考点:等差关系的确定;数列的函数特性;等差数列的通项公式.
点评:本题是中档题,考查数列的递推关系式的应用,数列通项公式与数列中最大项的求法,考查计算能力,转化思想,分类讨论的应用.

练习册系列答案
相关题目
 的前
的前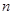 项和为
项和为
 ,对于任意的
,对于任意的 恒有
恒有

 的通项公式
的通项公式
 证明:
证明:
 的首项
的首项 ,且
,且 (
( )
) ,求证:数列
,求证:数列 为等差数列;②设
为等差数列;②设 ,求数列
,求数列 的前
的前 项和
项和 。
。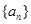 前n项和
前n项和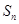 ,且
,且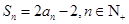 .
. ,求数列
,求数列 的前
的前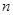 项和
项和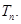
 是等差数列,公差
是等差数列,公差 ,
, 是
是 项和,已知
项和,已知 .
. ;
; =
= ,求数
,求数 列的前
列的前 .
.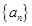 的前四项和为10,且
的前四项和为10,且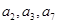 成等比数列
成等比数列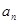 (2)设
(2)设 ,求数列
,求数列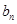 的前
的前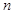 项和
项和
 和函数
和函数 ,若
,若 ,则称
,则称 上的函数
上的函数 满足:对任意
满足:对任意 ,都有
,都有 ,且
,且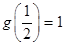 ;又数列
;又数列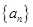 满足:
满足: .
.  是数列
是数列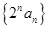 的母函数;
的母函数;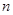 和
和 .
. 是数列
是数列 的母函数,且
的母函数,且 .若数列
.若数列 的前
的前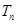 ,求证:
,求证: .
.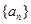 中,
中,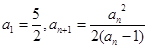
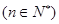 ,用数学归纳法证明:
,用数学归纳法证明: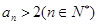 。
。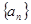 的通项公式为
的通项公式为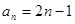 ,数列
,数列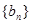 的前n项和为
的前n项和为 ,且满足
,且满足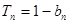
 中是否存在使得
中是否存在使得 是
是