题目内容
设数列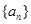 前n项和
前n项和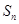 ,且
,且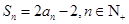 .
.
(Ⅰ)试求数列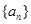 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前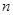 项和
项和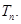
(Ⅰ) (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)当 时,
时,
所以, 即
即 3分
3分
当 时,
时, 4分
4分
由等比数列的定义知,数列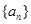 是首项为2,公比为2的等比数列,
是首项为2,公比为2的等比数列,
所以,数列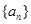 的通项公式为
的通项公式为 6分
6分
(Ⅱ)由(Ⅰ)知 8分
8分
所以 ,①
,①
以上等式两边同乘以 得
得 ②
②
①-②,得
 , 所以
, 所以 . 14分
. 14分
考点:数列求通项求和
点评:第一问中数列求通项用到了 ,第二问数列求和用到了错位相减法,此法适用于通项公式为关于
,第二问数列求和用到了错位相减法,此法适用于通项公式为关于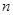 的一次式与指数式的乘积形式的数列,这两个考点都是数列题目中的高频考点,须加以重视
的一次式与指数式的乘积形式的数列,这两个考点都是数列题目中的高频考点,须加以重视

练习册系列答案
相关题目
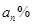 ,B喷雾器中药水的浓度为
,B喷雾器中药水的浓度为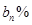 .
.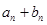 是一个常数;
是一个常数; 与
与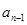 的关系式;
的关系式;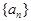 是等差数列,且
是等差数列,且 ,
, ,
, ,求数列
,求数列 前n项和
前n项和 .
. 是数列
是数列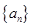 的前
的前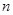 项和,且对任意
项和,且对任意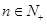 ,有
,有 ,
,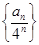 的通项公式;
的通项公式; 的前
的前 .
. ,数列
,数列 满足
满足 。
。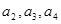 ;
;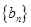 满足
满足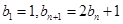 ,若数列
,若数列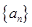 满足:
满足: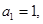 ,且当
,且当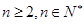 时,
时,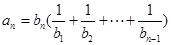
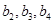 及
及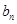 ;
; ,(注:
,(注: ).
).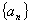 中,
中,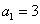 ,满足
,满足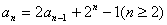 。
。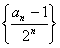 为等差数列;
为等差数列;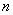 项和
项和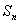 .
.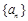 的前
的前 项和为
项和为 ,
, ,
, ,
,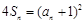 ,
, .
.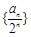 的前
的前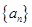 的前
的前 项和为
项和为 ,
,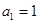 ,
,
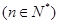 ,等差数列
,等差数列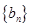 满足
满足 .
. ,求证
,求证 .
.