题目内容
将一根长为12m的铁丝弯折成一个矩形框架，则矩形框架的最大面积是（ ）
| A、9m2 |
| B、36m2 |
| C、45m2 |
| D、不存在 |
考点：基本不等式
专题：函数的性质及应用
分析：设框架的一边长为xm，根据矩形的周长为定值12m，求出框架面积的表达式，进而根据二次函数的图象和性质或者基本不等式法，可得框架的最大面积
解答：
解：设框架的一边长为xm，则另一边长为（6-x）m，则0＜x＜6．
设框架面积为ym2，
则y=x（6-x）=-x2+6x，
法1：y=x（6-x）=-x2+6x=-（x-3）2+9（0＜x＜6），
故当x=3时，ymax=9（m2）．
法2：∵0＜x＜6，∴6-x＞0，
∴由基本不等式得y=x（6-x）≤(
)2=9，
当且仅当x=6-x，即x=3时取等号，
∴当x=3时，ymax=9（m2）．
故选：A
设框架面积为ym2，
则y=x（6-x）=-x2+6x，
法1：y=x（6-x）=-x2+6x=-（x-3）2+9（0＜x＜6），
故当x=3时，ymax=9（m2）．
法2：∵0＜x＜6，∴6-x＞0，
∴由基本不等式得y=x（6-x）≤(
| x+6-x |
| 2 |
当且仅当x=6-x，即x=3时取等号，
∴当x=3时，ymax=9（m2）．
故选：A
点评：本题考查的知识点是二次函数的性质以及基本不等式的应用，其中根据已知求出框架面积的表达式，是解答的关键．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知数列{an}为等差数列，a1∈（0，1），a2∈（1，2），a3∈（2，3），则a4的取值范围是（ ）
| A、（3，4） | ||||
B、（2
| ||||
| C、（3，9） | ||||
D、（
|
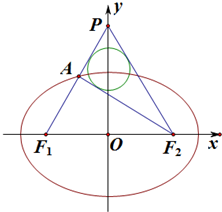已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=
+
的定义域是（ ）
| x-1 |
| 4-x |
| A、∅ |
| B、（-∞，1）∪[4，+∞） |
| C、（1，4） |
| D、[1，4] |