Question

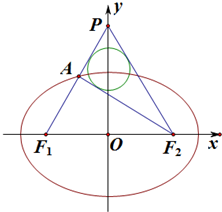已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的左右焦点分别为F₁，F₂，|F₁F₂|=

10

，P是y轴正半轴上一点，PF₁交椭圆于点A，若AF₂⊥PF₁，且△APF₂的内切圆半径为

2

2

，则椭圆的离心率是（　　）

• A、

  5

  4

• B、

  5

  3

• C、

  5

  10

• D、

  15

  4

Answer 1

考点：椭圆的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：由题意，直角三角形的内切圆半径r=

2

2

，结合|F₁F₂|=

10

，可得|AF1|2+|AF2|2=10，从而可求|AF₁|+|AF₂|=3

2

=2a，即可求得椭圆的离心率．

解答： 解：由题意，直角三角形的内切圆半径r=

PA+AF2-PF2

2

=

PA-PF1+AF2

2

=

AF2-AF1

2

=

2

2

，
∵|F₁F₂|=

10

，
∴|AF1|2+|AF2|2=10，
∴2|AF₁||AF₂|=8，
∴(|AF1|+|AF2|)2=18，
∴|AF₁|+|AF₂|=3

2

=2a，
∵|F₁F₂|=

10

，
∴椭圆的离心率是e=

c

a

=

10

3 2

=

5

3

．
故选B．

点评：本题考查椭圆的几何性质，考查椭圆的定义，考查学生分析解决问题的能力，属于中档题．