题目内容
 为了帮助小型企业乙转型发展,大型国企甲将经营状况良好的某种消费品专卖批发店,以120万元的优惠价格转让给了企业乙,并约定从该店经营的利润中,首先保证所有职工每月工资开支10万元,再逐步偿还转让费(不计息),在国企甲提供的资料中显示:①这种消费品的进价为每件20元;②该店月销量Q(千件)与销售价格x(元)的关系如图所示;③每月需水电房租等各种开支22000元.
为了帮助小型企业乙转型发展,大型国企甲将经营状况良好的某种消费品专卖批发店,以120万元的优惠价格转让给了企业乙,并约定从该店经营的利润中,首先保证所有职工每月工资开支10万元,再逐步偿还转让费(不计息),在国企甲提供的资料中显示:①这种消费品的进价为每件20元;②该店月销量Q(千件)与销售价格x(元)的关系如图所示;③每月需水电房租等各种开支22000元.(Ⅰ)求该店月销量Q(千件)与销售价格x(元)的函数关系式;
(Ⅱ)企业乙依靠该店,最早可望在多少月后能还清转让费?
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:(I)根据每月销售量Q(千件)与销售价格x(元)的关系是一条折线,是一个分段函数,每段是一个一次函数,根据线段两端点可求出解析式;
(Ⅱ)分段求出函数的最大值,比较后可得答案.
(Ⅱ)分段求出函数的最大值,比较后可得答案.
解答:
解:(I)由图可得该函数一个分段函数,每段是一个一次函数
在[22,32]上,直线过点(22,32),(32,12),则Q=-2x+76;
在[32,36]上,直线过点(32,12),(36,6),则Q=-
x+60,
∴Q=
;
(Ⅱ)设企业销售消费品所产生的利润为y千元,则
22≤x≤32时,y=(-2x+76)(x-20)=-2(x2-58x+760),
∴x=29时,ymax=162(千元);
32≤x≤36时,y=(-
x+60)(x-20)=-
(x2-60x+800),
∴x=32时,ymax=144(千元);
∴x=29时,ymax=162(千元),
∴16200-100000-22000-40000=4(万元),
∴每月最大偿还为4万元,最早可望在30个月后能还清转让费.
在[22,32]上,直线过点(22,32),(32,12),则Q=-2x+76;
在[32,36]上,直线过点(32,12),(36,6),则Q=-
| 3 |
| 2 |
∴Q=
|
(Ⅱ)设企业销售消费品所产生的利润为y千元,则
22≤x≤32时,y=(-2x+76)(x-20)=-2(x2-58x+760),
∴x=29时,ymax=162(千元);
32≤x≤36时,y=(-
| 3 |
| 2 |
| 3 |
| 2 |
∴x=32时,ymax=144(千元);
∴x=29时,ymax=162(千元),
∴16200-100000-22000-40000=4(万元),
∴每月最大偿还为4万元,最早可望在30个月后能还清转让费.
点评:本题考查分段函数的应用,突出考查二次函数的最值,考查分类讨论思想与运算能力,属于难题.

练习册系列答案
相关题目
若a>1,设函数f(x)=ax+x-2的零点为m,g(x)=logax+x-2的零点为n,则
+
的取值范围是( )
| 1 |
| m |
| 1 |
| n |
| A、(2,+∞) | ||
B、(
| ||
| C、(4,+∞) | ||
D、(
|
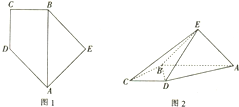 已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合,AB⊥BC且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连结EC、ED,得到四棱锥E-ABCD(如图2)
已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合,AB⊥BC且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连结EC、ED,得到四棱锥E-ABCD(如图2)