题目内容
数列4，7，10，13…（3n+1）按照如下方式排列
4
13 10 7
16 19 22 25 28
…
第i行第j的记作ai-j例如 a3-3=22，a3-4=25
则a20-4的值是（ ）
4
13 10 7
16 19 22 25 28
…
第i行第j的记作ai-j例如 a3-3=22，a3-4=25
则a20-4的值是（ ）
| A、1192 | B、1310 |
| C、1201 | D、70 |
考点：归纳推理,进行简单的合情推理
专题：规律型,等差数列与等比数列
分析：观察发现：是连续的整数排列，且第n行有2n-1个数，前19行共有数字1+3+5+…+37=381个，所以a20-4是数列bn=3n+1的397项，代入可得答案．
解答：
解：第1行有1个数字；
第2行有3个数字；
第3行有5个数字；
…
第n行有2n-1个数字；
故前n行共有1+3+5+…+（2n-1）=
=n2个数字，
故前19行共有192=361个数字，
由第20的数字从左到右倒序排列，
故a20-4是397个数字，
即a20-4是数列bn=3n+1的397项，
故a20-4=b397=3×397+1=1192，
故选：A
第2行有3个数字；
第3行有5个数字；
…
第n行有2n-1个数字；
故前n行共有1+3+5+…+（2n-1）=
| n[1+(2n-1)] |
| 2 |
故前19行共有192=361个数字，
由第20的数字从左到右倒序排列，
故a20-4是397个数字，
即a20-4是数列bn=3n+1的397项，
故a20-4=b397=3×397+1=1192，
故选：A
点评：本题考查的知识点是归纳推理，等差数列的通项公式，此题要发现各行的数字个数和行数的关系，从而进行分析计算．
练习册系列答案
备战中考寒假系列答案
相关题目
已知△ABC的三个顶点A，B，C及所在平面内一点P满足
+2
+3
=
，则△BCP的面积与△ABP的面积之比为（ ）
| BC |
| BA |
| PB |
| 0 |
| A、2：1 | B、3：1 |
| C、3：2 | D、1：2 |
已知P（-1，y）是角θ终边上一点，且sinθ=
，则y的值（ ）
2
| ||
| 5 |
| A、2 | B、-2 | C、±2 | D、1 |
若a＞1，设函数f（x）=ax+x-2的零点为m，g（x）=logax+x-2的零点为n，则
+
的取值范围是（ ）
| 1 |
| m |
| 1 |
| n |
| A、（2，+∞） | ||
B、（
| ||
| C、（4，+∞） | ||
D、（
|
函数y=x2-2x的单调递增区间是（ ）
| A、（1，+∞） |
| B、（-1，+∞） |
| C、（-∞，1） |
| D、（0，2） |
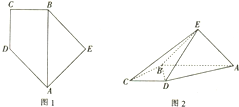已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合，AB⊥BC且AB=2CD=2BC（如图1），将此图形沿AB折叠成直二面角，连结EC、ED，得到四棱锥E-ABCD（如图2）