题目内容
已知双曲线C:
-
=1(a>0,b>0)离心率为3,直线y=2与双曲线C的两个交点间的距离为
,则双曲线C的方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| A、2x2-y2=1 | ||||
B、x2-
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用直线y=2与双曲线C的两个交点间的距离为
,可得2a2(b2+4)=3b2,根据离心率为3,可得b2=8a2,求出a2=1,b2=8,即可得到双曲线C的方程.
| 6 |
解答:
解:y=2时,
-
=1,∴x=±
,
∵直线y=2与双曲线C的两个交点间的距离为
,
∴2•
=
,
∴2a2(b2+4)=3b2,
∵离心率为3,
∴
=9,
∴b2=8a2,
∴a2=1,b2=8,
∴双曲线C的方程是x2-
=1.
故选:B.
| x2 |
| a2 |
| 4 |
| b2 |
| a |
| b |
| b2+4 |
∵直线y=2与双曲线C的两个交点间的距离为
| 6 |
∴2•
| a |
| b |
| b2+4 |
| 6 |
∴2a2(b2+4)=3b2,
∵离心率为3,
∴
| a2+b2 |
| a2 |
∴b2=8a2,
∴a2=1,b2=8,
∴双曲线C的方程是x2-
| y2 |
| 8 |
故选:B.
点评:本题考查双曲线的方程与性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
双曲线x2-4y2=4的离心率为( )
A、
| ||||
B、
| ||||
C、4
| ||||
D、
|
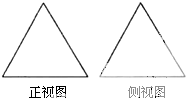 如图是两个全等的正三角形,给定下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中真命题的个数是( )
如图是两个全等的正三角形,给定下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中真命题的个数是( )| A、3 | B、2 | C、1 | D、0 |
已知数列{an}满足a1=1,a2=2,an+2=(1+cos2
)an+sin2
,则该数列的前18项和为( )
| nπ |
| 2 |
| nπ |
| 2 |
| A、2101 | B、2012 |
| C、1012 | D、1067 |
对于定义域为D的函数y=f(x)和常数C,若对任意正实数ξ,存在x∈D,使得0<|f(x)-c|<ξ恒成立,则称函数y=f(x)为“敛C函数”.现给出如下函数:
①f(x)=x(x∈Z); ②f(x)=(
)x+1(x∈Z);③f(x)=log2x;
其中为“敛1函数”的有( )
①f(x)=x(x∈Z); ②f(x)=(
| 1 |
| 2 |
其中为“敛1函数”的有( )
| A、② | B、①③ | C、②③ | D、①③ |
若实数x,y满足条件
,则x-2y的最小值是( )
|
| A、-3 | B、-2 | C、-1 | D、0 |
