题目内容
6.已知x>2y>0,且满足$\frac{x}{2}+\frac{1}{y}+\frac{8}{x-2y}$=10.则实数x的最大值为18.分析 由条件可得$\frac{2}{2y}$+$\frac{8}{x-2y}$=10-$\frac{1}{2}$x,即有[2y+(x-2y)]($\frac{2}{2y}$+$\frac{8}{x-2y}$)=(10-$\frac{1}{2}$x)x,将等式左边展开,运用基本不等式可得x的二次不等式,解不等式可得x的最大值.
解答 解:x>2y>0,且满足$\frac{x}{2}+\frac{1}{y}+\frac{8}{x-2y}$=10,
可得$\frac{2}{2y}$+$\frac{8}{x-2y}$=10-$\frac{1}{2}$x,
即有[2y+(x-2y)]($\frac{2}{2y}$+$\frac{8}{x-2y}$)=(10-$\frac{1}{2}$x)x,
可得10+$\frac{2(x-2y)}{2y}$+$\frac{16y}{x-2y}$=(10-$\frac{1}{2}$x)x≥10+2$\sqrt{\frac{2(x-2y)}{2y}•\frac{16y}{x-2y}}$=18,
当且仅当x-2y=4y,即x=6y,取得等号.
即有x2-20x+36≤0,
解得2≤x≤18.
可得x的最大值18.
故答案为:18.
点评 本题考查最值的求法,注意运用变形和基本不等式,考查转化思想,转化为x的二次不等式,考查运算能力,属于中档题.

练习册系列答案
相关题目

 B.
B. C.
C. D.
D.
 满足
满足 则
则 的最大值等于( )
的最大值等于( ) B.
B. C.
C. D.
D.
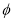 ,求k的取值范围.
,求k的取值范围. 将一块边长为6cm的正方形纸片,先按如图1所示的阴影部分截去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个正四棱锥模型(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥),将该四棱锥如图2放置,若其正视图为正三角形,则其体积为$\frac{8\sqrt{6}}{3}$cm3.
将一块边长为6cm的正方形纸片,先按如图1所示的阴影部分截去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个正四棱锥模型(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥),将该四棱锥如图2放置,若其正视图为正三角形,则其体积为$\frac{8\sqrt{6}}{3}$cm3.