题目内容
15.若二项式($\sqrt{x}$+$\frac{1}{x}$)n的展开式中各项的系数和为32,则该展开式中含x的系数为( )| A. | 1 | B. | 5 | C. | 10 | D. | 20 |
分析 令x=1,则2n=32,解得n=5,再利用通项公式即可得出.
解答 解:令x=1,则2n=32,解得n=5,
∴$(\sqrt{x}+\frac{1}{x})^{5}$的通项公式:Tr+1=${∁}_{5}^{r}(\sqrt{x})^{5-r}(\frac{1}{x})^{r}$=${∁}_{5}^{r}$${x}^{\frac{5}{2}-\frac{3r}{2}}$,
令$\frac{5}{2}-\frac{3r}{2}$=1,解得r=1.
∴该展开式中含x的系数为${∁}_{5}^{1}$=5.
故选:B.
点评 本题考查了二项式定理的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
7.已知随机变量ξ~B(3,$\frac{1}{2}$),则E(ξ)=( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
20.已知抛物线y2=4x上一动点M(x,y),定点N(0,1),则x+|MN|的最小值是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$-1 | D. | $\sqrt{2}$-1 |
7.已知圆C1:x2+y2+2x+8y-8=0与直线x+2y-1=0相交于两点A,B两点,则弦长|AB|=( )
| A. | 10 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
3.不等式x2-4x+3<0的解集为( )
| A. | (1,3) | B. | (-3,-1) | C. | (-∞,-3)∪(-1,+∞) | D. | (-∞,1)∪(3,+∞) |
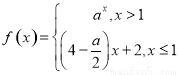 是R上的单调递增函数,则实数a的取值范围为( )
是R上的单调递增函数,则实数a的取值范围为( )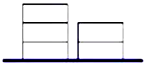 如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).
如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).