题目内容
18.设函数f(x)=$\frac{(x+2)^{2}+sinx}{{x}^{2}+4}$的最大值为M,最小值为m,则M+m=2.分析 化f(x)为1+$\frac{4x+sinx}{{x}^{2}+4}$,由g(x)=$\frac{4x+sinx}{{x}^{2}+4}$,定义域为R,判断g(x)的奇偶性,由图象性质可得g(x)的最值之和为0,进而得到所求和.
解答 解:函数f(x)=$\frac{(x+2)^{2}+sinx}{{x}^{2}+4}$
=$\frac{{x}^{2}+4+4x+sinx}{{x}^{2}+4}$=1+$\frac{4x+sinx}{{x}^{2}+4}$,
由g(x)=$\frac{4x+sinx}{{x}^{2}+4}$,定义域为R,
可得g(-x)+g(x)=$\frac{-4x-sinx}{{x}^{2}+4}$+$\frac{4x+sinx}{{x}^{2}+4}$=0,
可得g(x)为奇函数,
由奇函数的图象关于原点对称,
可得g(x)的最大值a与最小值b的和为0,
则M+m=a+1+b+1=(a+b)+2=2.
故答案为:2.
点评 本题考查函数的最值的求法,注意运用转化法,由奇函数的性质:最值之和为0,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.已知角α满足条件sin2α<0,sinα-cosα<0,则α在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知随机变量ξ~B(3,$\frac{1}{2}$),则E(ξ)=( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
7.已知圆C1:x2+y2+2x+8y-8=0与直线x+2y-1=0相交于两点A,B两点,则弦长|AB|=( )
| A. | 10 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
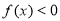 ,且f(1)=﹣2
,且f(1)=﹣2