题目内容
15.已知tan(α+$\frac{π}{4}$)=2(Ⅰ)求tanα的值;
(Ⅱ)求$\frac{sin2α-si{n}^{2}α}{1+cos2α}$的值.
分析 (Ⅰ)由已知利用两角和的正切函数公式即可求值得解.
(Ⅱ)由于tan$α=\frac{1}{3}$,利用二倍角公式,同角三角函数基本关系式化简所求即可计算得解.
解答 (本题满分为8分)
解:(Ⅰ)∵tan(α+$\frac{π}{4}$)=$\frac{tanα+1}{1-tanα}$=2,
∴解得:tan$α=\frac{1}{3}$…4分
(Ⅱ)∵tan$α=\frac{1}{3}$,
∴$\frac{sin2α-si{n}^{2}α}{1+cos2α}$=$\frac{2sinαcosα-si{n}^{2}α}{2co{s}^{2}α}$=$\frac{2tanα-ta{n}^{2}α}{2}$=$\frac{2×\frac{1}{3}-(\frac{1}{3})^{2}}{2}$=$\frac{5}{18}$…8分
点评 本题主要考查了两角和的正切函数公式,二倍角公式,同角三角函数基本关系式在三角函数化简求值中的由于,考查了转化思想,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
10.已知角α满足条件sin2α<0,sinα-cosα<0,则α在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.周末甲乙两同学相约看电影,约定7点到8点在电影院门口会面,先到者等20分钟,若另一人还未到就先进场,设两人在这段时间内的各时刻到达是等可能的,且两人互不影响,则两人能在电影院门口会面的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
7.已知随机变量ξ~B(3,$\frac{1}{2}$),则E(ξ)=( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
3.不等式x2-4x+3<0的解集为( )
| A. | (1,3) | B. | (-3,-1) | C. | (-∞,-3)∪(-1,+∞) | D. | (-∞,1)∪(3,+∞) |
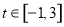 ,则输出的s属于( )
,则输出的s属于( )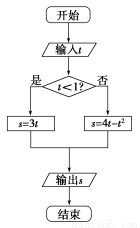
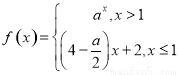 是R上的单调递增函数,则实数a的取值范围为( )
是R上的单调递增函数,则实数a的取值范围为( )