题目内容
7.己知O为坐标原点,倾斜角为$\frac{2π}{3}$的直线l与x,y轴的正半轴分别相交于点A,B,△AOB的面积为8$\sqrt{3}$.(I )求直线l的方程;
(II)直线l′过点O且与l平行,点P在l′上,求|PA|+|PB|的最小值.
分析 (I)由题意可得:直线l的斜率k=tan$\frac{2π}{3}$=-$\sqrt{3}$,设直线l的方程为:y=-$\sqrt{3}$x+b.可得直线l与坐标轴的正半轴交点为A$(\frac{\sqrt{3}}{3}b,0)$,B(0,b),其中b>0.可得S△OAB=$\frac{1}{2}×\frac{\sqrt{3}}{3}$b×b=8$\sqrt{3}$,解得b即可得出.
(II)由(I)可得:A(4,0),B(0,4$\sqrt{3}$).直线l′的方程为:y=-$\sqrt{3}$x.设点A关于直线l′的对称点A′(m,n),则$\left\{\begin{array}{l}{\frac{n-0}{m-4}=\frac{\sqrt{3}}{3}}\\{\frac{n}{2}=-\sqrt{3}•\frac{m+4}{2}}\end{array}\right.$,解得A′(-2,-2$\sqrt{3}$).|PA|+|PB|=|PA′|+|PB′|,当A′,B,P三点共线时,|PA|+|PB|取得最小值.即可得出.
解答 解:(I)由题意可得:直线l的斜率k=tan$\frac{2π}{3}$=-$\sqrt{3}$,设直线l的方程为:y=-$\sqrt{3}$x+b.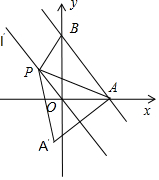
可得直线l与坐标轴的正半轴交点为A$(\frac{\sqrt{3}}{3}b,0)$,B(0,b),其中b>0.
∴S△OAB=$\frac{1}{2}×\frac{\sqrt{3}}{3}$b×b=8$\sqrt{3}$,解得b=4$\sqrt{3}$.
∴直线l的方程为:y=-$\sqrt{3}$x+4$\sqrt{3}$.
(II)由(I)可得:A(4,0),B(0,4$\sqrt{3}$).
直线l′的方程为:y=-$\sqrt{3}$x.
设点A关于直线l′的对称点A′(m,n),
则$\left\{\begin{array}{l}{\frac{n-0}{m-4}=\frac{\sqrt{3}}{3}}\\{\frac{n}{2}=-\sqrt{3}•\frac{m+4}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-2}\\{n=-2\sqrt{3}}\end{array}\right.$,∴A′(-2,-2$\sqrt{3}$).
∵|PA|+|PB|=|PA′|+|PB′|,
∴当A′,B,P三点共线时,|PA|+|PB|取得最小值.
∴(|PA|+|PB|)min=|A′B|=4$\sqrt{7}$.
点评 本题考查了直线方程、垂直平分线的性质、方程组的解法、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

| A. | -5 | B. | 5 | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
| A. | 5+$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 5-$\sqrt{2}$ |
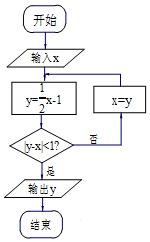
| A. | 0 | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | -1 |