题目内容
8.已知P是椭圆$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1和双曲线x2-y2=2的一个交点,若F1、F2分别是椭圆的左、右焦点,则cos∠F1PF2=90°.分析 不妨设点P在第一象限,|F1F2|=4.则|PF1|+|PF2|=2$\sqrt{6}$,|PF1|-|PF2|=2$\sqrt{2}$,可得|PF1|,|PF2|.再利用余弦定理即可得出.
解答 解:不妨设点P在第一象限,
|F1F2|=4.
则|PF1|+|PF2|=2$\sqrt{6}$,|PF1|-|PF2|=2$\sqrt{2}$,
∴|PF1|=$\sqrt{6}$$+\sqrt{2}$,|PF2|=$\sqrt{6}$-$\sqrt{2}$.
∴cos∠F1PF2=$\frac{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-|{F}_{1}{F}_{2}{|}^{2}}{2|P{F}_{1}||P{F}_{2}|}$=$\frac{(\sqrt{6}+\sqrt{2})^{2}+(\sqrt{6}-\sqrt{2})^{2}-{4}^{2}}{2(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})}$=0,
∴∠F1PF2=90°.
故答案为:90°.
点评 本题考查了椭圆与双曲线的定义、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若$sinA=\frac{{2\sqrt{2}}}{3}$,a=2,ccosB+bcosC=2acosB,则b的值为( )
| A. | $2\sqrt{6}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{6}}}{4}$ |
20.已知两定点A(-3,0),B(3,0),如果动点P满足|PA|=2|PB|,则点P的轨迹所包围的图形的面积等于( )
| A. | π | B. | 4π | C. | 9π | D. | 16π |
17.某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
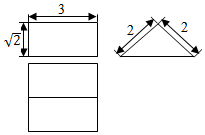

| A. | $\frac{17\sqrt{17}}{6}$π | B. | 34π | C. | 17π | D. | $\frac{17}{4}$π |
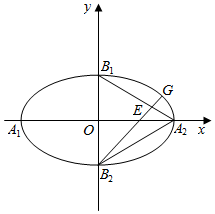 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点是A1,A2,B1,B2,△A2B1B2是边长为2的正三角形.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点是A1,A2,B1,B2,△A2B1B2是边长为2的正三角形.