题目内容
20．已知两定点A（-3，0），B（3，0），如果动点P满足|PA|=2|PB|，则点P的轨迹所包围的图形的面积等于（ ）| A． | π | B． | 4π | C． | 9π | D． | 16π |
分析 设出P点坐标，根据|PA|=2|PB|列出方程整理出P的轨迹方程，判断图形计算面积．
解答 解：设P（x，y），则|PA|=$\sqrt{（x+3）^{2}+{y}^{2}}$，|PB|=$\sqrt{（x-3）^{2}+{y}^{2}}$，
∵|PA|=2|PB|，∴（x+3）2+y2=4[（x-3）2+y2]，即x2+y2-10x+9=0，化为标准式方程得（x-5）2+y2=16．
即P的轨迹所包围的图形为半径为4的圆，该圆的面积S=π×42=16π．
故选：D．
点评 本题考查了轨迹方程的求法，属于基础题．
练习册系列答案
相关题目
11．函数$f（x）=\frac{1}{ln（2x+1）}$的定义域是（ ）
| A． | $（-\frac{1}{2}，+∞）$ | B． | $（-\frac{1}{2}，0）∪（0，+∞）$ | C． | $[-\frac{1}{2}，+∞）$ | D． | [0，+∞） |
15．若直线l1：ax+2y+6=0与直线l2：x+（a-1）y-1=0垂直，则实数a=（ ）
| A． | $\frac{2}{3}$ | B． | -1 | C． | 2 | D． | -1或2 |
12．已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，直线l与椭圆交于与椭圆相交于A、B两点，点P（1，1）是线段AB的中点，则直线l的斜率为（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{3}{4}$ | D． | $\frac{3}{4}$ |
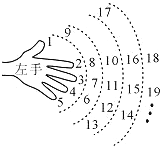如图，一个小朋友按如图所示的规则练习数数，1大拇指，2食指，3中指，4无名指，5小指，6无名指，…，一直数到2015时，对应的指头是中指（填指头的名称）．
10．已知数列{an}的通项公式为an=$\frac{n}{n+1}$，则数列{an}是（ ）
| A． | 递减数列 | B． | 递增数列 | C． | 常数列 | D． | 摆动数列 |