题目内容
13.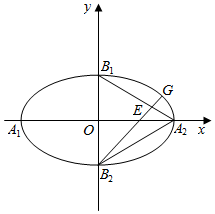 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点是A1,A2,B1,B2,△A2B1B2是边长为2的正三角形.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点是A1,A2,B1,B2,△A2B1B2是边长为2的正三角形.(1)求椭圆的方程;
(2)若G是椭圆上在第一象限内的动点,直线B1G交线段A2B2于点E,求$\frac{|G{B}_{1}|}{|E{B}_{1}|}$的取值范围.
分析 (1)由正三角形的定义和性质可得b=1,a=$\frac{\sqrt{3}}{2}$•2b,解得a,b,即可得到所求椭圆方程;
(2)设直线B1G的方程为:y=kx-1,(k>$\frac{\sqrt{3}}{3}$),与椭圆的方程联立解得G,可得|GB1|.直线A2B2的方程为:$\frac{x}{\sqrt{3}}$+y=1与y=kx-1联立解得E.可得|EB1|,可得$\frac{|G{B}_{1}|}{|E{B}_{1}|}$=$\frac{3{k}^{2}+\sqrt{3}k}{1+3{k}^{2}}$,变形利用不等式的性质及基本不等式,即可得出范围.
解答 解:(1)由△A2B1B2是边长为2的正三角形,
可得2b=2,a=$\frac{\sqrt{3}}{2}$•2b
即有a=$\sqrt{3}$,b=1,
可得椭圆的方程为$\frac{{x}^{2}}{3}$+y2=1;
(2)B1(0,-1),A2($\sqrt{3}$,0),B2(0,1),
设直线B1G的方程为:y=kx-1,(k>$\frac{\sqrt{3}}{3}$).
联立$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+3{y}^{2}=3}\end{array}\right.$,化为(1+3k2)x2-6kx=0,
解得G($\frac{6k}{1+3{k}^{2}}$,$\frac{3{k}^{2}-1}{3{k}^{2}+1}$)
∴|GB1|=$\sqrt{(\frac{6k}{1+3{k}^{2}})^{2}+(\frac{6{k}^{2}}{1+3{k}^{2}})^{2}}$
=$\frac{6k\sqrt{1+{k}^{2}}}{1+3{k}^{2}}$,
直线A2B2的方程为:$\frac{x}{\sqrt{3}}$+y=1,
联立$\left\{\begin{array}{l}{y=kx-1}\\{y=1-\frac{\sqrt{3}}{3}x}\end{array}\right.$,解得E($\frac{6}{3k+\sqrt{3}}$,$\frac{3k-\sqrt{3}}{3k+\sqrt{3}}$),
∴|EB1|=$\sqrt{(\frac{6}{3k+\sqrt{3}})^{2}+(\frac{6k}{3k+\sqrt{3}})^{2}}$=$\frac{6\sqrt{1+{k}^{2}}}{3k+\sqrt{3}}$,
∴$\frac{|G{B}_{1}|}{|E{B}_{1}|}$=$\frac{3{k}^{2}+\sqrt{3}k}{1+3{k}^{2}}$=1+$\frac{1}{(\sqrt{3}k-1)+\frac{2}{\sqrt{3}k-1}+2}$,
由k>$\frac{\sqrt{3}}{3}$,可得$\sqrt{3}$k-1>0,即有$\frac{|G{B}_{1}|}{|E{B}_{1}|}$>1,
由($\sqrt{3}$k-1)+$\frac{2}{\sqrt{3}k-1}$≥2$\sqrt{(\sqrt{3}k-1)•\frac{2}{\sqrt{3}k-1}}$=2$\sqrt{2}$,
当且仅当k=$\frac{\sqrt{2}+1}{\sqrt{3}}$时取得等号,
即有$\frac{|G{B}_{1}|}{|E{B}_{1}|}$≤1+$\frac{1}{2\sqrt{2}+2}$=$\frac{\sqrt{2}+1}{2}$.
则$\frac{|G{B}_{1}|}{|E{B}_{1}|}$的取值范围是(1,$\frac{\sqrt{2}+1}{2}$].
点评 本题考查了椭圆与圆的标准方程及其性质、直线交点问题、两点之间的距离公式,考查了基本不等式的运用,以及推理能力与计算能力,属于中档题.

| A. | $\sqrt{10}$ 或$\frac{{2\sqrt{2}}}{3}$ | B. | $\sqrt{10}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$或$\sqrt{10}$ |
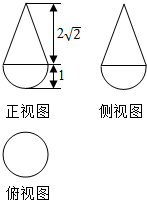
| A. | 6π | B. | 5π | C. | 4π | D. | 3π |