题目内容
已知a=(log34)2,b=log43,c=ln
,下列结论正确的是( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、c>a>b |
| D、b>a>c |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用对数函数的单调性求解.
解答:
解:∵a=(log34)2>(log33)2=1,
0=log41<b=log43<log44=1,
c=ln
<log2
=log43=b,
∴a>b>c.
故选:B.
0=log41<b=log43<log44=1,
c=ln
| 3 |
| 3 |
∴a>b>c.
故选:B.
点评:本题考查三个数的大小的比较,是基础题,解题时要注意对数函数的单调性的合理运用.

练习册系列答案
相关题目
函数y=
在定义域内是( )
| lgcosx |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
执行如图所示的程序框图,若f(x)=3x2-1,取?=
,则输出的值为( )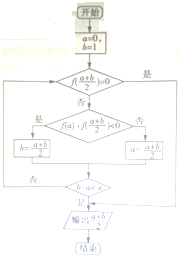
| 1 |
| 10 |

A、
| ||
B、
| ||
C、
| ||
D、
|