题目内容
直线l过点P（1，1），且到A（1，4），B（3，2）两点的距离相等，这样的直线有 条．
考点：两点间的距离公式
专题：直线与圆
分析：可知当直线平行于直线AB时，或过AB的中点时满足题意，进而可得答案．
解答：
解：∵点P（1，1），A（1，4），B（3，2），
∴kPA不存在，kPB=
，
故P点不在直线AB上，
若直线l过点P（1，1），且到A（1，4），B（3，2）两点的距离相等，
则直线l与直线AB平行，或过线段AB的中点，
故这样的直线有2条，
故答案为：2
∴kPA不存在，kPB=
| 1 |
| 2 |
故P点不在直线AB上，
若直线l过点P（1，1），且到A（1，4），B（3，2）两点的距离相等，
则直线l与直线AB平行，或过线段AB的中点，
故这样的直线有2条，
故答案为：2
点评：本题考查平面直线与直线的位置关系，点到直线的距离，分类讨论是解决问题的关键，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知命题P：?x∈（0，
），使得cosx≤x，则该命题是否定为（ ）
| π |
| 2 |
A、?x∈（0，
| ||
B、?x∈（0，
| ||
C、?x∈（0，
| ||
D、?x∈（0，
|
下列命题是真命题的是（ ）
| A、-1的平方根只有一个 |
| B、i是1的四次方根 |
| C、i是-1的立方根 |
| D、i是方程x2-1的根 |
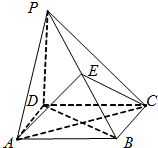如图，四棱锥P-ABCD的底面ABCD是菱形，∠BAD=60°，PD⊥底面ABCD，点E在棱PB上．
如图，在棱长为4的正方体ABCDA1B1C1D1中，P是A1B1上一点，且PB1=| 1 |
| 4 |
A、
| ||
B、
| ||
| C、4 | ||
| D、16 |