题目内容
已知圆C过点A(a,b),圆心C(c,0),且a2b2+a2+c2-4a-8ab-2c+21=0,则圆C的标准方程为 .
考点:圆的标准方程
专题:计算题,直线与圆
分析:利用配方法,可得(ab-4)2+(a-2)2+(c-1)2=0,从而可得圆C过点A(2,2),圆心C(1,0),即可求出圆C的标准方程.
解答:
解:∵a2b2+a2+c2-4a-8ab-2c+21=0,
∴(ab-4)2+(a-2)2+(c-1)2=0,
∴a=b=2,c=1,
∴圆C过点A(2,2),圆心C(1,0),
∴r=
,
∴圆C的标准方程为(x-1)2+y2=5.
故答案为:(x-1)2+y2=5.
∴(ab-4)2+(a-2)2+(c-1)2=0,
∴a=b=2,c=1,
∴圆C过点A(2,2),圆心C(1,0),
∴r=
| 5 |
∴圆C的标准方程为(x-1)2+y2=5.
故答案为:(x-1)2+y2=5.
点评:本题考查圆C的标准方程,考查学生的计算能力,比较基础.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
当x∈(0,
)时,函数f(x)=tx-sinx(t∈R)的值恒小于0,则t的取值范围是( )
| π |
| 2 |
A、t≤
| ||
B、t≤
| ||
C、t≥
| ||
D、t<
|

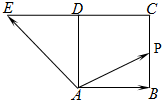 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若动点P从点A出发,沿正方形的边按如下路线运动:A→B→C→D→E→A→D,其中
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若动点P从点A出发,沿正方形的边按如下路线运动:A→B→C→D→E→A→D,其中 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点