题目内容
已知f（x）=ln（x-cosx+a），若?x0＞0，使f（f（x0））=x0，则实数a的取值范围为 ．
考点：函数的零点与方程根的关系
专题：计算题,导数的概念及应用
分析：由题意，f（x0）=x0，则ln（x-cosx+a）=x，可得a=ex-x+cosx，构造h（x）=ex-x+cosx，函数在（0，+∞）上单调递增，即可求出实数a的取值范围．
解答：
解：由题意，f（x0）=x0，则ln（x-cosx+a）=x，
∴x-cosx+a=ex，
∴a=ex-x+cosx，
设h（x）=ex-x+cosx，
则h′（x）=ex-1-sinx，
∴函数在（0，+∞）上单调递增，
∴h（x）＞h（0）=2，
∴a＞2
故答案为：（2，+∞）．
∴x-cosx+a=ex，
∴a=ex-x+cosx，
设h（x）=ex-x+cosx，
则h′（x）=ex-1-sinx，
∴函数在（0，+∞）上单调递增，
∴h（x）＞h（0）=2，
∴a＞2
故答案为：（2，+∞）．
点评：本题考查求实数a的取值范围，考查导数知识的运用，正确分离参数是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
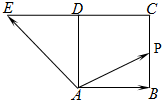如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若动点P从点A出发，沿正方形的边按如下路线运动：A→B→C→D→E→A→D，其中