题目内容
在△ABC中,角A,B,C的对边分别为a,b,c.已知
=
,A+3C=π.
(1)求cosC的值;
(2)求sinB的值;
(3)若b=3
,求△ABC的面积.
| b |
| c |
2
| ||
| 3 |
(1)求cosC的值;
(2)求sinB的值;
(3)若b=3
| 3 |
考点:正弦定理,三角函数中的恒等变换应用
专题:计算题,解三角形
分析:(1)由题意可得B=2C.又由正弦定理及已知得
=
,即可得解.
(2)由C∈(0,π),可得sinC,根据sinB=sin2C即可求值.
(3)由B=2C,可得cosB,又A+B+C=π,可求sinA=sin(B+C),由
=
,b=3
,可得C,由面积公式即可得解.
2
| ||
| 3 |
| 2sinCcosC |
| sinC |
(2)由C∈(0,π),可得sinC,根据sinB=sin2C即可求值.
(3)由B=2C,可得cosB,又A+B+C=π,可求sinA=sin(B+C),由
| b |
| c |
2
| ||
| 3 |
| 3 |
解答:
解:(1)因为A+B+C=π,A+3C=π,
所以B=2C. …(2分)
又由正弦定理,得
=
,
=
,
=
,
化简得,cosC=
. …(5分)
(2)因为C∈(0,π),所以sinC=
=
=
.
所以sinB=sin2C=2sinCcosC=2×
×
=
. …(8分)
(3)因为B=2C,
所以cosB=cos2C=2cos2C-1=2×
-1=-
. …(10分)
因为A+B+C=π,
所以sinA=sin(B+C)=sinBcosC+cosBsinC=
×
+(-
)×
=
.
…(12分)
因为
=
,b=3
,所以c=
.
所以△ABC的面积S=
bcsinA=
×3
×
×
=
. …(14分)
所以B=2C. …(2分)
又由正弦定理,得
| b |
| sinB |
| c |
| sinC |
| b |
| c |
| sinB |
| sinC |
2
| ||
| 3 |
| 2sinCcosC |
| sinC |
化简得,cosC=
| ||
| 3 |
(2)因为C∈(0,π),所以sinC=
| 1-cos2C |
1-
|
| ||
| 3 |
所以sinB=sin2C=2sinCcosC=2×
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
(3)因为B=2C,
所以cosB=cos2C=2cos2C-1=2×
| 1 |
| 3 |
| 1 |
| 3 |
因为A+B+C=π,
所以sinA=sin(B+C)=sinBcosC+cosBsinC=
2
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 9 |
…(12分)
因为
| b |
| c |
2
| ||
| 3 |
| 3 |
| 9 |
| 2 |
所以△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 9 |
| 2 |
| ||
| 9 |
9
| ||
| 4 |
点评:本题主要考查了正弦定理,二倍角公式,同角三角函数关系式,三角形面积公式的应用,属于基础题.

练习册系列答案
相关题目
已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),若f(-1)>-2,f(-7)=
,则实数a的取值范围为( )
| a+1 |
| 3-2a |
A、(-
| ||
| B、(-2,1) | ||
C、(1,
| ||
D、(-∞,1)∪(
|
过点(1,2)且斜率为3的直线方程为( )
| A、y=3x-3 |
| B、y=3x-2 |
| C、y=3x-1 |
| D、y=x-1 |
直线x+
y-1=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
“t=1”是“双曲线
-
=1的离心率为2”的( )
| x2 |
| t |
| y2 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
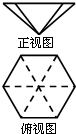 已知一个底面为正六边形,侧棱长都相等的六棱锥的正视图与俯视图如图所示,若该几何体的底面边长为2,侧棱长为
已知一个底面为正六边形,侧棱长都相等的六棱锥的正视图与俯视图如图所示,若该几何体的底面边长为2,侧棱长为