题目内容
14.已知函数f(x)=ex-ax-1,g(x)=ln(ex-1)-lnx,若存在m>0,使f(g(m))>f(m)成立,则a的取值范图是(1,+∞).分析 当x>0时,ex-1>x,故对?x>0,g(x)>0;构造函数H(x)=xex-ex+1(x>0),则H′(x)=xex>0;从而由导数求得a的范围.
解答 解:ex-x-1的导数为ex-1,当x>0时,y=ex-x-1递增,
即有ex-1>x,故对?x>0,g(x)>0;
构造函数H(x)=xex-ex+1(x>0),则H′(x)=xex>0;
故函数H(x)在(0,+∞)上单调递增,
则H(x)>H(0),
则?x>0,xex-ex+1>0成立,
即g(x)<x在x>0时恒成立,
当a>1时,ex-ax-1的导数为ex-a,f(x)在(lna,+∞)上单调递增,
在(0,lna)上单调递减,
当0<x<lna时,0<g(x)<x<lna,
所以f(g(x))>f(x),
所以满足题意的a的取值范围是(1,+∞).
故答案为:(1,+∞).
点评 本题考查了导数的综合应用:求单调区间,考查单调性的运用和存在性问题的解法,属于中档题.

练习册系列答案
相关题目
4.在二项式${({\sqrt{x}+\frac{1}{{2•\root{6}{x}}}})^n}$的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
9.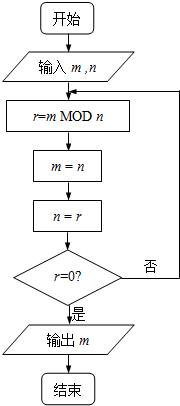 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )
 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )| A. | 0 | B. | 5 | C. | 45 | D. | 90 |
19.某化工厂产生的废气经过过滤后排放,以模型$y={P_0}{e^{-kx}}$去拟合过滤过程中废气的污染物数量ymg/L与时间xh间的一组数据时,为了求出回归方程,设z=lny,其变换后得到线性回归方程z=-0.5x+2+ln300,则当经过6h后,预报废气的污染物数量为( )
| A. | 300e2mg/L | B. | 300emg/L | C. | $\frac{300}{e^2}$mg/L | D. | $\frac{300}{e}$mg/L |
3.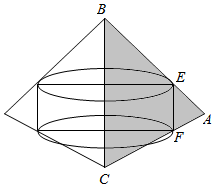 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2大小关系不确定 |
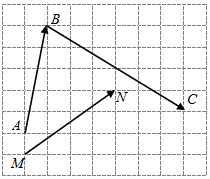 向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.
向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.