题目内容
15．
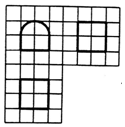如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中曲线部分是圆弧，则此几何体的表面积为（ ）| A． | 10+2π | B． | 12+3π | C． | 20+4π | D． | 16+5π |
分析 由三视图知几何体是上部为半圆柱体，下部为长方体的组合体，结合图中数据求出它的表面积．
解答 解：由三视图知，
该几何体是上部为半圆柱体，下部为长方体的组合体，
其表面积为
S=S长方体+S半圆柱
=（1×2×2+2×1×2+22）+（π•12+π•1•2）
=12+3π．
故选：B．
点评 本题主要考查了利用三视图求几何体表面积的应用问题，是基础题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
5．方程${2^{{{log}_3}x}}=\frac{1}{4}$的解为（ ）
| A． | 9 | B． | $\sqrt{3}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{1}{9}$ |
6．某校为了解学生对正在进行的一项教学改革的态度，从500名高一学生和400名高二学生中按分层抽样的方式抽取了45名学生进行问卷调查，结果可以分成以下三类：支持、反对、无所谓，调查结果统计如下：
（1）（i）求出表中的x，y的值；
（ii）从反对的同学中随机选取2人进一步了解情况，求恰好高一、高二各1人的概率；
（2）根据表格统计的数据，完成下面的2×2的列联表，并判断是否有90%的把握认为持支持与就读年级有关．（不支持包括无所谓和反对）
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
| 支持 | 无所谓 | 反对 | |
| 高一年级 | 18 | x | 2 |
| 高二年级 | 10 | 6 | y |
（ii）从反对的同学中随机选取2人进一步了解情况，求恰好高一、高二各1人的概率；
（2）根据表格统计的数据，完成下面的2×2的列联表，并判断是否有90%的把握认为持支持与就读年级有关．（不支持包括无所谓和反对）
| 高一年级 | 高二年级 | 总计 | |
| 支持 | |||
| 不支持 | |||
| 总计 |
| P（K2≥k0） | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
10．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞1}\\{（\frac{1}{2}）^{x}，x≤1}\end{array}\right.$，则f（f（-$\frac{1}{2}$））=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |
7．双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1的焦点到其渐近线的距离为（ ）
| A． | 2 | B． | 3 | C． | $\sqrt{3}$ | D． | 4 |