题目内容
5．已知抛物线C：y2=2px（p＞0），直线$l：y=\sqrt{3}（{x-1}）$，l与C交于A，B两点，若$AB=\frac{16}{3}$，则p=（ ）| A． | 8 | B． | 4 | C． | 2 | D． | 1 |
分析 直线$l：y=\sqrt{3}（{x-1}）$与抛物线y2=2px联立，可得3x2+（-6-2p）x+3=0，利用$AB=\frac{16}{3}$，求出p，即可得出结论．
解答 解：直线$l：y=\sqrt{3}（{x-1}）$与抛物线y2=2px联立，可得3x2+（-6-2p）x+3=0，
∵$AB=\frac{16}{3}$，
∴$\sqrt{1+3}$•$\sqrt{（\frac{-6-2p}{3}）^{2}-4}$=$\frac{16}{3}$，
∴p=2，
故选C．
点评 本题考查抛物线方程，考查直线与抛物线的位置关系，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
15．
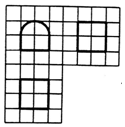如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中曲线部分是圆弧，则此几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中曲线部分是圆弧，则此几何体的表面积为（ ）| A． | 10+2π | B． | 12+3π | C． | 20+4π | D． | 16+5π |
20．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的焦距为4$\sqrt{5}$，渐近线方程为2x±y=0，则双曲线的方程为（ ）
| A． | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | B． | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | C． | $\frac{x^2}{16}-\frac{y^2}{64}=1$ | D． | $\frac{x^2}{64}-\frac{y^2}{16}=1$ |
14．
某程序框图如图所示，则该程序运行后输出的值是（ ）
某程序框图如图所示，则该程序运行后输出的值是（ ）| A． | 2 | B． | -3 | C． | 5 | D． | -1 |
已知函数f（x）=|x+1|-|x-3|．