题目内容
11．若集合A={x|-x2+2x≤0}，B={x|x＞1}，则A∪B等于（ ）| A． | [2，+∞） | B． | [0，+∞） | C． | （1，2] | D． | （-∞，0]∪（1，+∞） |
分析 先求出集合A，B的对应元素，根据集合关系和运算即可得到结论．
解答 解：-x2+2x≤0即x（x-2）≥0，解得x≤0或x≥2，故A=（-∞，0]∪[2，+∞），
B={x|x＞1}=（1，+∞），
∴A∪B=（-∞，0]∪（1，+∞），
故选：D．
点评 本题主要考查集合的基本运算，利用不等式的解法求出集合A是解决本题的关键，比较基础．
练习册系列答案
相关题目
16．计算$\frac{1+i}{i}$+（2-i）2等于（ ）
| A． | 4-5i | B． | 3-4i | C． | 5-4i | D． | 4-3i |
3．若数列{an}中，a1=$\frac{1}{2}$，an+1+2an=0（n∈N*），则S5=（ ）
| A． | -$\frac{11}{2}$ | B． | -$\frac{31}{6}$ | C． | $\frac{11}{2}$ | D． | $\frac{31}{6}$ |
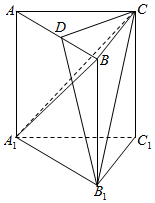如图，在直三棱柱ABC-A1B1C1中，AC=BC=CC1，AC⊥BC，点D是AB的中点．