题目内容
3.若数列{an}中,a1=$\frac{1}{2}$,an+1+2an=0(n∈N*),则S5=( )| A. | -$\frac{11}{2}$ | B. | -$\frac{31}{6}$ | C. | $\frac{11}{2}$ | D. | $\frac{31}{6}$ |
分析 直接利用等差数列的求和公式计算即得结论.
解答 解:∵an+1+2an=0(n∈N*),
∴an+1=-2an(n∈N*),
又∵a1=$\frac{1}{2}$,
∴数列{an}是首项为$\frac{1}{2}$、公比分为-2的等比数列,
∴Sn=$\frac{\frac{1}{2}[1-(-2)^{n}]}{1-(-2)}$=$\frac{1-(-2)^{n}}{6}$,
∴S5=$\frac{1-(-2)^{5}}{6}$=$-\frac{31}{6}$,
故选:B.
点评 本题考查数列的通项及前n项和,考查等比数列的求和公式,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
11.若集合A={x|-x2+2x≤0},B={x|x>1},则A∪B等于( )
| A. | [2,+∞) | B. | [0,+∞) | C. | (1,2] | D. | (-∞,0]∪(1,+∞) |
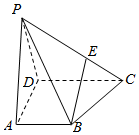 如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.
如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.