题目内容
6.将1440°化为弧度,结果是8π.分析 利用1°=$\frac{π}{180°}$弧度即可得出.
解答 解:1440°=1440°×$\frac{π}{180°}$=8π弧度.
故答案为:8π.
点评 本题考查了角度与弧度的互化,属于基础题.

练习册系列答案
相关题目
14.规定:f″(x)=(f′(x))′,例如,f(x)=x2,f′(x)=2x,f″(x)=2,设g(x)=lnx,函数h(x)=mg″(x)+g′(x)一$\frac{π}{3}$,下列结论正确的是( )
| A. | 当m∈$(\frac{2}{3},+∞)$时,函数h(x)无零点 | |
| B. | 当m∈$(-∞,\frac{2}{3})$时,函数h(x)恰有一个零点 | |
| C. | 当m∈$[0,\frac{2}{3}]$时,函数h(x)恰有两个零点 | |
| D. | 当m∈$(-\frac{2}{3},\frac{2}{3})$时,函数h(x)恰有三个零点 |
11.已知f(x)=$\frac{(a+1)x+a}{x+1}$,且f(x-1)的图象的对称中心是(0,3),则f′(2)的值为( )
| A. | -$\frac{1}{9}$ | B. | $\frac{1}{9}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
1.将函数f(x)=sin(2x+θ)(-$\frac{π}{2}$<θ<$\frac{π}{2}$)的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P(0,$\frac{\sqrt{3}}{2}$),则φ的值可以是( )
| A. | $\frac{5π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
18.已知点(1,3)和(-4,-2)在直线2x-y+m=0的两侧,则m的取值范围是( )
| A. | m<1或m>6 | B. | m=1或m=6 | C. | 1<m<6 | D. | 1≤m≤6 |
19.已知i是虚数单位,若(2-i)•z=i3,则$\overline z$=( )
| A. | $\frac{1}{5}$-$\frac{2}{5}$i | B. | -$\frac{2}{5}$+$\frac{1}{5}$i | C. | -$\frac{2}{5}$-$\frac{1}{5}$i | D. | $\frac{1}{5}$+$\frac{2}{5}$i |
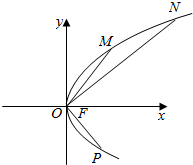 已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.
已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.