题目内容
10.已知函数f(x)=ex|x-1|-2ax+3a恰有3个零点,则实数a的取值范围是$(-\frac{{\sqrt{e}}}{4},0)$.分析 利用函数的零点个数,画出两个函数的图象,通过函数的导数,通过切线的斜率关系,求解新函数的极值,推出a的范围.
解答 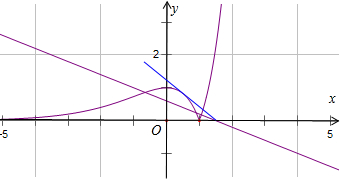 解:函数f(x)=ex|x-1|-2ax+3a恰有3个零点,就是函数y=ex|x-1|,与函数y=2ax-3a有3个交点.
解:函数f(x)=ex|x-1|-2ax+3a恰有3个零点,就是函数y=ex|x-1|,与函数y=2ax-3a有3个交点.
当x>1时y=ex(x-1),是增函数.
x=0时,y=0.
当x<1时,函数y=ex|x-1|=ex(1-x),
y′=-xex,x<0时,y′>0,函数是增函数,
x∈(0,1)时,函数是减函数,
函数y=ex|x-1|的图象如图,设y=2ax-3a,与y=ex(1-x)的切点为:(x,ex(1-x)),
可得:$\frac{{e}^{x}(1-x)}{x-\frac{3}{2}}=2a$,x∈(0,1),
即a=$\frac{{e}^{x}(1-x)}{2x-3}$,
a′=$\frac{[{e}^{x}(1-x)]′(2x-3)-2{e}^{x}(1-x)}{(2x-3)^{2}}$=$-\frac{{e}^{x}}{(2x-3)^{2}}$(2x2-5x+2),
令a′=0可得2x2-5x+2=0,解得x=$\frac{1}{2}$,x=2舍去.
x∈(0,$\frac{1}{2}$),a是减函数,x∈($\frac{1}{2},1$)时,a是增函数,a的最小值为:$\frac{{e}^{\frac{1}{2}(1-\frac{1}{2})}}{2×\frac{1}{2}-3}$=$-\frac{\sqrt{e}}{4}$.
可得a∈($-\frac{\sqrt{e}}{4}$,0)
故答案为:($-\frac{\sqrt{e}}{4}$,0).
点评 本题考查函数的零点个数的判断,函数的导数的应用,考查转化思想数形结合以及计算能力.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案| A. | 15 | B. | 12 | C. | 9 | D. | 与k的取值有关 |
| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
| A. | (-3,0) | B. | (3,0) | C. | (-1,3) | D. | (-2,0) |
| A. | $\frac{π}{3}(4+14\sqrt{2})$ | B. | $\frac{{14\sqrt{2}π}}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{4π}{3}$ |
| A. | {x>-2011} | B. | {x|x<-2011} | C. | {x|-2011<x<0} | D. | {x|-2016<x<-2011} |
| A. | y=sinx | B. | y=log2|x| | C. | y=x2-$\frac{1}{2}$ | D. | y=$\frac{1}{x}$ |